教師なし学習

教師なし学習は機械学習のフレームワークであり、教師あり学習とは対照的に、アルゴリズムはラベルなしデータからのみパターンを学習します。^[1]教師あり学習の範囲における他のフレームワークには、データのごく一部にタグが付けられる弱教師または半教師あり学習や、自己教師あり学習などがあります。一部の研究者は、自己教師あり学習を教師なし学習の一形態と見なしています。^[2]

概念的には、教師なし学習は、データ、トレーニング、アルゴリズム、および下流のアプリケーションの側面に分かれます。通常、データセットは、Web クロールによって取得された大規模なテキストコーパスなど、わずかなフィルタリング ( Common Crawlなど) のみで、安価に「自然のまま」収集されます。これは、データセット ( ImageNet1000など) が通常手動で構築され、はるかにコストがかかる教師あり学習と比較して有利です。

k-meansのようなクラスタリングアルゴリズム、主成分分析 (PCA)のような次元削減技術、ボルツマン機械学習、オートエンコーダなど、教師なし学習専用に設計されたアルゴリズムがありました。ディープラーニングの台頭後、大規模な教師なし学習のほとんどは、適切なトレーニング手順を設計して教師なし学習を実行できるように適応させた勾配降下法によって汎用ニューラルネットワークアーキテクチャをトレーニングすることによって行われています。

訓練されたモデルはそのまま使用できる場合もありますが、多くの場合は下流のアプリケーションに合わせて変更されます。たとえば、生成的事前訓練法では、テキストデータセットを生成するようにモデルを訓練し、その後、テキスト分類などの他のアプリケーションに合わせて微調整します。^[3]^[4]別の例として、オートエンコーダは優れた特徴に訓練され、潜在拡散モデルなどの他のモデルのモジュールとして使用できます。

タスク

タスクは、多くの場合、識別的(認識) または生成的(想像)に分類されます。多くの場合、識別タスクでは教師あり学習が使用され、生成タスクでは教師なし学習が使用されます (ベン図を参照)。ただし、この区別は非常に曖昧です。たとえば、物体認識では教師あり学習が適していますが、教師なし学習でも物体をグループにクラスタリングできます。さらに、進歩が進むにつれて、一部のタスクでは両方の方法を使用し、一部のタスクでは一方から他方へと移行します。たとえば、画像認識は、最初は強力な教師あり学習として始まりましたが、教師なし事前トレーニングを採用することでハイブリッドになり、その後、ドロップアウト、ReLU、適応学習率の出現により、再び教師あり学習に移行しました。

典型的な生成タスクは次のとおりです。各ステップで、データセットからデータポイントがサンプリングされ、データの一部が削除され、モデルは削除された部分を推測する必要があります。これは、ノイズ除去オートエンコーダとBERT の場合に特に顕著です。

ニューラルネットワークアーキテクチャ

トレーニング

学習フェーズでは、教師なしネットワークは与えられたデータを模倣しようとし、模倣した出力のエラーを使用して自分自身を修正します (つまり、重みとバイアスを修正します)。エラーは、誤った出力が発生する可能性が低いこととして表現される場合もあれば、ネットワーク内の不安定な高エネルギー状態として表現される場合もあります。

教師あり学習法では主にバックプロパゲーションが使用されますが、教師なし学習ではホップフィールド学習則、ボルツマン学習則、対比発散、覚醒睡眠、変分推論、最大尤度、最大事後確率、ギブスサンプリング、およびバックプロパゲーション再構築エラーまたは隠れ状態の再パラメータ化などの他の方法も使用されます。詳細については、下の表を参照してください。

エネルギー

エネルギー関数は、ネットワークの活性化状態のマクロ的な尺度です。ボルツマンマシンでは、コスト関数の役割を果たします。この物理学との類似性は、ルートヴィヒ・ボルツマンが気体のマクロなエネルギーを粒子の運動のミクロな確率から分析したことに触発されたものです。ここで、kはボルツマン定数、T は温度です。RBMネットワークでは、関係は、^[5]であり、およびはすべての可能な活性化パターンとにわたって変化します。より正確には、であり、ここではすべてのニューロン（可視および非表示）の活性化パターンです。そのため、初期のニューラルネットワークにはボルツマンマシンという名前が付けられています。ポール・スモレンスキーはハーモニーと呼んでいます。ネットワークは、高いハーモニーである低エネルギーを探します。 $p\propto e^{-E/kT}$ $p=e^{-E}/Z$ $p$ $E$ $\textstyle {Z=\sum _{\scriptscriptstyle {\text{All Patterns}}}e^{-E({\text{pattern}})}}$ $p(a)=e^{-E(a)}/Z$ $a$ $-E\,$

ネットワーク

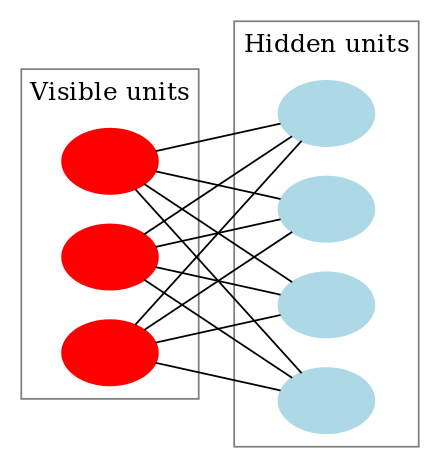
この表は、さまざまな教師なしネットワークの接続図を示しています。詳細については、「ネットワークの比較」のセクションで説明します。円はニューロンで、円間のエッジは接続の重みです。ネットワーク設計が変化すると、新機能を有効にするために機能が追加されたり、学習を高速化するために機能が削除されたりします。たとえば、ニューロンは、堅牢な出力を可能にするために決定論的 (ホップフィールド) と確率論的 (ボルツマン) の間で変更され、学習を高速化するためにレイヤー内で重みが削除され (RBM)、接続が非対称になることが許可されます (ヘルムホルツ)。

ホップフィールド	ボルツマン	RBM の	スタックドボルツマン
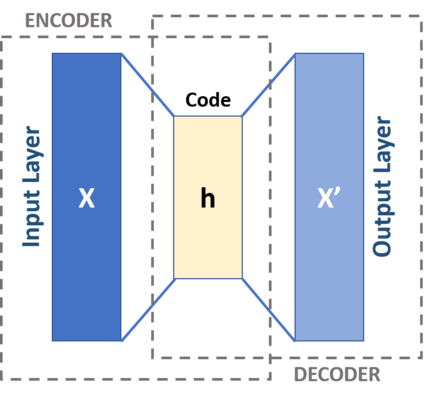
単一の自己接続層を持つ鉄の磁気ドメインに基づくネットワーク。コンテンツアドレス指定可能なメモリとして使用できます。	ネットワークは 2 つのレイヤー (非表示と表示) に分割されますが、対称的な双方向の重みが依然として使用されます。ボルツマンの熱力学に従い、個々の確率によってマクロなエネルギーが生成されます。	制限付きボルツマンマシン。これは、分析を扱いやすくするために、レイヤー内の横方向の接続が禁止されているボルツマンマシンです。	このネットワークには、隠れた特徴の階層をエンコードするための複数の RBM があります。単一の RBM をトレーニングした後、別の青い隠れ層 (左側の RBM を参照) が追加され、上位 2 つの層が赤と青の RBM としてトレーニングされます。したがって、RBM の中間層は、トレーニングフェーズに応じて、非表示または表示として機能します。

ヘルムホルツ	オートエンコーダ	VA
スタックされたボルツマンマシンの双方向対称接続の代わりに、ループを形成するために個別の一方向接続があります。これは生成と識別の両方を行います。	入力された世界の適切な中間層表現を見つけることを目的としたフィードフォワードネットワーク。このネットワークは決定論的であるため、後継の VAE ほど堅牢ではありません。	オートエンコーダに変分推論を適用します。中間層は、ガウス分布の平均と分散のセットです。確率的な性質により、決定論的なオートエンコーダよりも堅牢な想像力が可能になります。

人の名前が付けられたネットワークのうち、ホップフィールドだけがニューラルネットワークを直接研究しました。ボルツマンとヘルムホルツは人工ニューラルネットワークより前に登場しましたが、彼らの物理学と生理学の研究は、使用された分析方法に影響を与えました。

歴史

1974	WA Little [de]が認知のために提案したイジング磁気モデル
1980	福島は、後に畳み込みニューラルネットワークと呼ばれることになるネオコグニトロンを紹介しました。これは主に SL で使用されますが、ここでも言及する価値があります。
1982	John Hopfield によってCAMおよび分類器として説明された Ising 変種 Hopfield ネット。
1983	Sherington と Kirkpatrick の 1975 年の研究に続いて HintonとSejnowskiによって記述された確率ニューロンを備えた Ising 変種ボルツマンマシン。
1986	ポール・スモレンスキーは、実質的に同じボルツマンエネルギー関数を持つ RBM であるハーモニー理論を発表しました。スモレンスキーは実践的なトレーニングスキームを提供しませんでした。ヒントンが 2000 年代半ばに提供しました。
1995	Schmidthuber は言語用のLSTMニューロンを紹介します。
1995	ダヤン＆ヒントンがヘルムホルツマシンを発表
2013	Kingma、Rezende らは、ニューラルネットをコンポーネントとするベイズグラフィカル確率ネットワークとして変分オートエンコーダを導入しました。

特定のネットワーク

ここでは、選択したネットワークのいくつかの特徴を紹介します。それぞれの詳細については、以下の比較表をご覧ください。

ホップフィールドネットワーク: 強磁性からヒントを得たホップフィールドネットワーク。ニューロンは上下の 2 進磁気モーメントを持つ鉄ドメインに対応し、ニューラル接続はドメインの相互影響に対応します。対称接続により、グローバルなエネルギー定式化が可能になります。推論中、ネットワークは標準の活性化ステップ関数を使用して各状態を更新します。対称重みと適切なエネルギー関数により、安定した活性化パターンへの収束が保証されます。非対称重みは分析が困難です。ホップフィールドネットは、コンテンツアドレス可能メモリ (CAM) として使用されます。
ボルツマンマシン: これらは確率的ホップフィールドネットです。状態値は、このpdfから次のようにサンプリングされます。バイナリニューロンがベルヌーイ確率 p(1) = 1/3 で発火し、p(0) = 2/3 で休止するとします。一様分布の乱数 y を取り、それを逆累積分布関数に代入することでサンプリングします。この場合は、2/3 でしきい値が設定されたステップ関数です。逆関数 = { x <= 2/3 の場合は 0、 x > 2/3 の場合は 1 }。
シグモイド信念ネット: 1992 年に Radford Neal によって導入されたこのネットワークは、確率的グラフィカルモデルのアイデアをニューラルネットワークに適用します。重要な違いは、グラフィカルモデルのノードには事前に割り当てられた意味があるのに対し、Belief Net ニューロンの特徴はトレーニング後に決定されることです。このネットワークは、バイナリ確率ニューロンで構成される、疎に接続された有向非巡回グラフです。学習ルールは、p(X) の最大尤度から来ています: Δw _ij s _j * (s _i - p _i )、ここで p _i = 1 / ( 1 + e^{ニューロン i への重み付けされた入力})。s _jは、事後分布の偏りのないサンプルからの活性化であり、これは、Judea Perl によって提起された Explaining Away 問題のために問題となります。変分ベイズ法では、代理事後分布を使用し、この複雑さを露骨に無視します。 $\propto$
ディープビリーフネットワーク: Hinton によって導入されたこのネットワークは、RBM とシグモイドビリーフネットワークのハイブリッドです。上位 2 層は RBM で、2 層目以降はシグモイドビリーフネットワークを形成します。スタック RBM方式でトレーニングし、最上位 RBM より下の認識重みを削除します。2009 年現在、最適な深さは 3 ～ 4 層のようです。^[6]
ヘルムホルツマシン: これらは変分オートエンコーダの初期のインスピレーションです。2 つのネットワークが 1 つに統合され、前方重みが認識を操作し、後方重みが想像力を実行します。おそらく、両方を実行する最初のネットワークです。ヘルムホルツは機械学習には携わっていませんでしたが、「感覚入力の考えられる原因を推測する機能を持つ統計的推論エンジン」という考え方に影響を与えました。^[7]確率的バイナリニューロンは、状態が 0 または 1 である確率を出力します。データ入力は通常、レイヤーとは見なされませんが、ヘルムホルツマシン生成モードでは、データレイヤーは中間レイヤーから入力を受け取り、この目的のために個別の重みを持つため、レイヤーと見なされます。したがって、このネットワークには 3 つのレイヤーがあります。
変分オートエンコーダ: これらはヘルムホルツマシンにヒントを得たもので、確率ネットワークとニューラルネットワークを組み合わせたものです。オートエンコーダは 3 層の CAM ネットワークで、中間層は入力パターンの内部表現であると想定されています。エンコーダニューラルネットワークは確率分布 q _φ (z は x を基準) で、デコーダネットワークは p _θ (x は z を基準) です。重みは、ヘルムホルツの W と V ではなく、phi と theta と名付けられています。これは見た目の違いです。これらの 2 つのネットワークは完全に接続することも、別の NN スキームを使用することもできます。

ネットワークの比較

	ホップフィールド	ボルツマン	RBM の	スタックRBM	ヘルムホルツ	オートエンコーダ	VA
使用法と注目すべき点	CAM、巡回セールスマン問題	CAM。接続の自由度が高いため、このネットワークの分析は困難です。	パターン認識。MNIST の数字と音声で使用されます。	認識と想像力。教師なしの事前トレーニングおよび/または教師ありの微調整でトレーニングされます。	想像力、模倣	言語: 創作、翻訳。視覚: ぼやけた画像を強調する	現実的なデータを生成する
ニューロン	決定論的なバイナリ状態。活性化 = { x が負の場合は 0 (または -1)、それ以外の場合は 1 }	確率的バイナリホップフィールドニューロン	← 同じ。（2000年代半ばに実数値に拡張）	← 同じ	← 同じ	言語: LSTM。視覚: ローカル受容野。通常は実数値の relu 活性化。	中間層ニューロンは、ガウス分布の平均と分散をエンコードします。実行モード (推論) では、中間層の出力はガウス分布からサンプリングされた値になります。
接続	対称的な重みを持つ 1 層。自己接続はありません。	2 層。1 つは非表示、もう 1 つは表示。対称的な重み。	← 同じ。レイヤー内に横方向の接続はありません。	最上層は無向で対称です。他の層は双方向で非対称です。	3 層: 非対称の重み。2 つのネットワークが 1 つに結合されます。	3 層。入力は、入力重みがない場合でも層と見なされます。NLP の場合は再帰層、視覚の場合はフィードフォワード畳み込み。入力と出力のニューロン数は同じです。	3層: 入力、エンコーダー、分配サンプラーデコーダー。サンプラーは層とはみなされない
推論とエネルギー	エネルギーはギブスの確率測度によって与えられる: $E=-{\frac {1}{2}}\sum _{i,j}{w_{ij}{s_{i}}{s_{j}}}+\sum _{i}{\theta _{i}}{s_{i}}$	← 同じ	← 同じ		KLダイバージェンスを最小化する	推論はフィードフォワードのみです。以前のULネットワークは順方向と逆方向に実行されました	エラーを最小化する = 再構築エラー - KLD
トレーニング	Δw _ij = s _i *s _j、+1/-1ニューロンの場合	Δw _ij = e*(p _ij - p' _ij )。これはKLDを最小化することで導き出されます。e = 学習率、p' = 予測値、p = 実際の分布です。	Δw _ij = e*( < v _i h _j >_データ- < v _i h _j >_平衡)。これは、ギブスサンプリングによる対照的発散の一種です。"<>" は期待値です。	← 同様。一度に 1 層ずつトレーニングします。3 セグメントパスで平衡状態を近似します。バックプロパゲーションはありません。	覚醒-睡眠2段階トレーニング	再構築エラーを逆伝播する	バックプロパゲーションの隠れ状態を再パラメータ化する
強さ	物理システムに似ているので、その方程式を継承する	← 同じ。隠れたニューロンは外界の内部表現として働く	ボルツマンマシンよりも高速で実用的なトレーニングスキーム	素早くトレーニングします。階層的な機能を提供します	解剖学的にやや複雑。情報理論と統計力学で分析可能
弱点		横方向のつながりのため訓練が難しい	均衡には多くの反復が必要	整数および実数値ニューロンはより複雑です。

ヘブビアン学習、アート、SOM

ニューラルネットワークの研究における教師なし学習の古典的な例は、ドナルド・ヘブの原理、つまり、一緒に発火するニューロンは一緒に接続されるという原理である。^[8]ヘブ学習では、接続はエラーに関係なく強化されるが、2つのニューロン間の活動電位の一致のみの関数である。^[9]シナプスの重みを変更する同様のバージョンでは、活動電位間の時間（スパイクタイミング依存可塑性またはSTDP）を考慮に入れる。ヘブ学習は、パターン認識や経験学習などのさまざまな認知機能の基礎となると仮定されている。

ニューラルネットワークモデルの中で、自己組織化マップ（SOM）と適応共鳴理論（ART）は、教師なし学習アルゴリズムでよく使用されます。SOMは、マップ内の近くの場所が同様の特性を持つ入力を表す地形的組織です。ARTモデルでは、クラスターの数は問題のサイズに応じて変化し、ユーザーは警戒パラメータと呼ばれるユーザー定義の定数を使用して、同じクラスターのメンバー間の類似性の度合いを制御できます。ARTネットワークは、自動ターゲット認識や地震信号処理など、多くのパターン認識タスクに使用されます。^[10]

確率的手法

教師なし学習で使用される主な方法の2つは、主成分分析とクラスター分析です。クラスター分析は、アルゴリズムの関係を推定するために、共通の属性を持つデータセットをグループ化またはセグメント化するために教師なし学習で使用されます。^{[11]クラスター分析は、}ラベル付け、分類、またはカテゴリ化されていないデータをグループ化する機械学習の一分野です。フィードバックに応答する代わりに、クラスター分析はデータ内の共通点を識別し、それぞれの新しいデータにおけるそのような共通点の有無に基づいて反応します。このアプローチは、どちらのグループにも当てはまらない異常なデータポイントを検出するのに役立ちます。

教師なし学習の中心的な応用分野は統計学における密度推定の分野であるが^[12]、教師なし学習はデータの特徴の要約や説明を含む他の多くの領域を網羅している。教師あり学習と対比すると、教師あり学習は入力データのラベルに応じて条件付き確率分布を推測するのに対し、教師なし学習は事前確率分布を推測することになる。

アプローチ

教師なし学習で使用される最も一般的なアルゴリズムには、(1) クラスタリング、(2) 異常検出、(3) 潜在変数モデルを学習するためのアプローチなどがあります。各アプローチでは、次のようにいくつかの方法が使用されます。

クラスタリング手法には、階層的クラスタリング、^[13] k平均法、^[14] 混合モデル、モデルベースクラスタリング、DBSCAN、OPTICSアルゴリズムなどがある。
異常検出方法には、ローカル外れ値係数、分離フォレストなどがあります。
期待最大化アルゴリズム（EM）、モーメント法、ブラインド信号分離技術（主成分分析、独立成分分析、非負値行列分解、特異値分解）などの潜在変数モデルを学習するためのアプローチ

モーメント法

教師なし学習の統計的アプローチの 1 つに、モーメント法があります。モーメント法では、モデル内の未知のパラメータ (対象) は 1 つ以上のランダム変数のモーメントに関連付けられているため、これらの未知のパラメータはモーメントが与えられれば推定できます。モーメントは通常、サンプルから経験的に推定されます。基本的なモーメントは、1 次モーメントと 2 次モーメントです。ランダムベクトルの場合、1 次モーメントは平均ベクトル、2 次モーメントは共分散行列(平均が 0 の場合) です。高次のモーメントは通常、行列を多次元配列として高次のものに一般化したテンソルを使用して表されます。

特に、モーメント法は潜在変数モデルのパラメータ学習に有効であることが示されています。潜在変数モデルは、観測変数に加えて、観測されない潜在変数のセットも存在する統計モデルです。機械学習における潜在変数モデルの非常に実用的な例は、トピックモデリングです。これは、文書のトピック（潜在変数）に基づいて文書内の単語（観測変数）を生成する統計モデルです。トピックモデリングでは、文書のトピックが変更されると、文書内の単語は異なる統計パラメータに従って生成されます。モーメント法（テンソル分解技術）は、いくつかの仮定の下で、潜在変数モデルの大規模なクラスのパラメータを一貫して回復することが示されている。^[15]

期待値最大化アルゴリズム(EM) も、潜在変数モデルを学習するための最も実用的な方法の 1 つです。ただし、局所最適値に陥る可能性があり、アルゴリズムがモデルの真の未知のパラメータに収束することが保証されません。対照的に、モーメント法では、いくつかの条件下でグローバル収束が保証されます。

参照

参考文献

^ Wu, Wei. 「教師なし学習」（PDF）。2024年4月14日時点のオリジナルよりアーカイブ（PDF）。 2024年4月26日閲覧。
^ 劉暁;チャン、ファンジン。ホウ・ジェンユー。ミアン、リー。王、趙宇。張、静。唐潔（2021）。「自己教師あり学習: 生成的または対照的」。知識およびデータ工学に関する IEEE トランザクション: 1. arXiv : 2006.08218。土井：10.1109/TKDE.2021.3090866。ISSN 1041-4347。
^ Radford, Alec; Narasimhan, Karthik; Salimans, Tim; Sutskever, Ilya (2018年6月11日). 「生成的事前トレーニングによる言語理解の向上」(PDF) . OpenAI . p. 12. 2021年1月26日時点のオリジナルよりアーカイブ(PDF) . 2021年1月23日閲覧。
^ Li, Zhuohan; Wallace, Eric; Shen, Sheng; Lin, Kevin; Keutzer, Kurt; Klein, Dan; Gonzalez, Joey (2020-11-21). 「Train Big, Then Compress: Rethinking Model Size for Efficient Training and Inference of Transformers」第37回国際機械学習会議の議事録。PMLR: 5958–5968。
^ Hinton, G. (2012). 「制限付きボルツマンマシンのトレーニングに関する実践ガイド」(PDF) .ニューラルネットワーク: コツ.コンピュータサイエンスの講義ノート。第 7700 巻。Springer。pp. 599–619。doi :10.1007/ 978-3-642-35289-8_32。ISBN 978-3-642-35289-8. 2022年9月3日にオリジナルからアーカイブ（PDF）されました。2022年11月3日閲覧。
^ 「Deep Belief Nets」（ビデオ）2009年9月。2022年3月8日時点のオリジナルよりアーカイブ。2022年3月27日閲覧。 {{cite web}}:不明なパラメータ|people=は無視されました (ヘルプ)
^ Peter, Dayan ; Hinton, Geoffrey E. ; Neal, Radford M. ; Zemel, Richard S. (1995). 「ヘルムホルツマシン」. Neural Computation . 7 (5): 889–904. doi :10.1162/neco.1995.7.5.889. hdl : 21.11116/0000-0002-D6D3-E . PMID 7584891. S2CID 1890561.
^ Buhmann, J.; Kuhnel, H. (1992). 「競合ニューラルネットワークによる教師なしおよび教師ありデータクラスタリング」[議事録 1992] IJCNN 国際ニューラルネットワーク合同会議。第 4 巻。IEEE。pp. 796–801。doi :10.1109/ ijcnn.1992.227220。ISBN 0780305590. S2CID 62651220。
^ コメサーニャ＝カンポス、アルベルト;ブザ＝ロドリゲス、ホセ・ベニート（2016年6月）。「設計プロセスの意思決定におけるヘビアン学習の応用」。インテリジェント製造ジャーナル。27 (3): 487–506。土井：10.1007/s10845-014-0881-z。ISSN 0956-5515。S2CID 207171436。
^ Carpenter, GA & Grossberg, S. (1988). 「自己組織化ニューラルネットワークによる適応型パターン認識の技術」(PDF) . Computer . 21 (3): 77–88. doi :10.1109/2.33. S2CID 14625094. 2018-05-16にオリジナル(PDF)からアーカイブ。2013-09-16に取得。
^ Roman, Victor (2019-04-21). 「教師なし機械学習：クラスタリング分析」. Medium . 2020-08-21時点のオリジナルよりアーカイブ。2019-10-01に閲覧。
^ Jordan, Michael I.; Bishop, Christopher M. (2004). 「7. インテリジェントシステム § ニューラルネットワーク」。Tucker, Allen B. (編)。コンピュータサイエンスハンドブック (第 2 版)。Chapman & Hall/CRC Press。doi : 10.1201 / 9780203494455。ISBN 1-58488-360-X. 2022年11月3日時点のオリジナルよりアーカイブ。2022年11月3日閲覧。
^ ハスティー、ティブシラニ、フリードマン 2009、485-586 ページ
^ Garbade, Dr Michael J. (2018-09-12). 「機械学習におけるK平均法クラスタリングの理解」。Medium。2019年5月28日時点のオリジナルよりアーカイブ。2019年10月31日閲覧。
^ Anandkumar, Animashree; Ge, Rong; Hsu, Daniel; Kakade, Sham; Telgarsky, Matus (2014). 「潜在変数モデルを学習するためのテンソル分解」(PDF) . Journal of Machine Learning Research . 15 : 2773–2832. arXiv : 1210.7559 . Bibcode :2012arXiv1210.7559A. 2015-03-20 にオリジナルからアーカイブ(PDF)されました。2015-04-10に取得。

さらに読む

ブスケ、O.フォン・ルクスバーグ, アメリカ; Raetsch、G.編。 (2004)。機械学習に関する上級講義。スプリンガー。ISBN 978-3540231226。
Duda, Richard O. ; Hart, Peter E. ; Stork , David G. (2001)。「教師なし学習とクラスタリング」。パターン分類(第 2 版)。Wiley。ISBN 0-471-05669-3。
ハスティー、トレバー、ティブシラニ、ロバート、フリードマン、ジェローム (2009)。「教師なし学習」。統計学習の要素: データマイニング、推論、予測。シュプリンガー。pp. 485–586。doi :10.1007/978-0-387-84858-7_14。ISBN 978-0-387-84857-0. 2022年11月3日時点のオリジナルよりアーカイブ。2022年11月3日閲覧。
Hinton, Geoffrey ; Sejnowski , Terrence J.編 (1999)。教師なし学習: ニューラルコンピューティングの基礎。MITプレス。ISBN 0-262-58168-X。

[WeiWu-1] Wu, Wei. 「教師なし学習」（PDF）。2024年4月14日時点のオリジナルよりアーカイブ（PDF）。 2024年4月26日閲覧。

[2] 劉暁;チャン、ファンジン。ホウ・ジェンユー。ミアン、リー。王、趙宇。張、静。唐潔（2021）。「自己教師あり学習: 生成的または対照的」。知識およびデータ工学に関する IEEE トランザクション: 1. arXiv : 2006.08218。土井：10.1109/TKDE.2021.3090866。ISSN 1041-4347。

[gpt1paper-3] Radford, Alec; Narasimhan, Karthik; Salimans, Tim; Sutskever, Ilya (2018年6月11日). 「生成的事前トレーニングによる言語理解の向上」(PDF) . OpenAI . p. 12. 2021年1月26日時点のオリジナルよりアーカイブ(PDF) . 2021年1月23日閲覧。

[4] Li, Zhuohan; Wallace, Eric; Shen, Sheng; Lin, Kevin; Keutzer, Kurt; Klein, Dan; Gonzalez, Joey (2020-11-21). 「Train Big, Then Compress: Rethinking Model Size for Efficient Training and Inference of Transformers」第37回国際機械学習会議の議事録。PMLR: 5958–5968。

[Hinton2010-5] Hinton, G. (2012). 「制限付きボルツマンマシンのトレーニングに関する実践ガイド」(PDF) .ニューラルネットワーク: コツ.コンピュータサイエンスの講義ノート。第 7700 巻。Springer。pp. 599–619。doi :10.1007/ 978-3-642-35289-8_32。ISBN 978-3-642-35289-8. 2022年9月3日にオリジナルからアーカイブ（PDF）されました。2022年11月3日閲覧。

[HintonMlss2009-6] 「Deep Belief Nets」（ビデオ）2009年9月。2022年3月8日時点のオリジナルよりアーカイブ。2022年3月27日閲覧。 {{cite web}}:不明なパラメータ|people=は無視されました (ヘルプ)

[“nc95“-7] Peter, Dayan ; Hinton, Geoffrey E. ; Neal, Radford M. ; Zemel, Richard S. (1995). 「ヘルムホルツマシン」. Neural Computation . 7 (5): 889–904. doi :10.1162/neco.1995.7.5.889. hdl : 21.11116/0000-0002-D6D3-E . PMID 7584891. S2CID 1890561.

[Buhmann-8] ^ Buhmann, J.; Kuhnel, H. (1992). 「競合ニューラルネットワークによる教師なしおよび教師ありデータクラスタリング」[議事録 1992] IJCNN 国際ニューラルネットワーク合同会議。第 4 巻。IEEE。pp. 796–801。doi :10.1109/ ijcnn.1992.227220。ISBN 0780305590. S2CID 62651220。

[Comesana-9] コメサーニャ＝カンポス、アルベルト;ブザ＝ロドリゲス、ホセ・ベニート（2016年6月）。「設計プロセスの意思決定におけるヘビアン学習の応用」。インテリジェント製造ジャーナル。27 (3): 487–506。土井：10.1007/s10845-014-0881-z。ISSN 0956-5515。S2CID 207171436。

[Carpenter-10] Carpenter, GA & Grossberg, S. (1988). 「自己組織化ニューラルネットワークによる適応型パターン認識の技術」(PDF) . Computer . 21 (3): 77–88. doi :10.1109/2.33. S2CID 14625094. 2018-05-16にオリジナル(PDF)からアーカイブ。2013-09-16に取得。

[tds-ul-11] Roman, Victor (2019-04-21). 「教師なし機械学習：クラスタリング分析」. Medium . 2020-08-21時点のオリジナルよりアーカイブ。2019-10-01に閲覧。

[JordanBishop2004-12] Jordan, Michael I.; Bishop, Christopher M. (2004). 「7. インテリジェントシステム § ニューラルネットワーク」。Tucker, Allen B. (編)。コンピュータサイエンスハンドブック (第 2 版)。Chapman & Hall/CRC Press。doi : 10.1201 / 9780203494455。ISBN 1-58488-360-X. 2022年11月3日時点のオリジナルよりアーカイブ。2022年11月3日閲覧。

[Hastie-13] ハスティー、ティブシラニ、フリードマン 2009、485-586 ページ

[tds-kmeans-14] Garbade, Dr Michael J. (2018-09-12). 「機械学習におけるK平均法クラスタリングの理解」。Medium。2019年5月28日時点のオリジナルよりアーカイブ。2019年10月31日閲覧。

[TensorLVMs-15] Anandkumar, Animashree; Ge, Rong; Hsu, Daniel; Kakade, Sham; Telgarsky, Matus (2014). 「潜在変数モデルを学習するためのテンソル分解」(PDF) . Journal of Machine Learning Research . 15 : 2773–2832. arXiv : 1210.7559 . Bibcode :2012arXiv1210.7559A. 2015-03-20 にオリジナルからアーカイブ(PDF)されました。2015-04-10に取得。