普朗克定律

在物理学中，普朗克定律（也称为普朗克辐射定律^{[1] : 1305}）描述了当黑体与其环境之间没有物质或能量的净流动时，在给定温度T下处于热平衡状态的黑体所发射的电磁辐射的光谱密度。^[2]

19 世纪末，物理学家无法解释为何当时已精确测量的黑体辐射观测到的光谱在较高频率下与现有理论预测的光谱有显著差异。1900 年，德国物理学家马克斯·普朗克启发式地推导出观测光谱的公式，他假设一个假想的带电振荡器在包含黑体辐射的腔体中只能以最小增量E改变其能量，该增量与其相关电磁波的频率成正比。虽然普朗克最初认为将能量分成增量的假设是一种数学技巧，只是为了得到正确答案而引入的，但包括阿尔伯特·爱因斯坦在内的其他物理学家在他的工作的基础上进行了进一步的发展，现在人们认为普朗克的见解对量子理论具有根本重要性。

每个物理物体都会自发地、持续地发射电磁辐射，物体的光谱辐射率B _ν描述的是特定辐射频率下每单位面积、每单位立体角和每单位频率的光谱发射功率。根据普朗克辐射定律，随着温度的升高，物体的总辐射能量会增加，发射光谱的峰值会向更短的波长移动。^[3]根据普朗克分布定律，给定温度下的光谱能量密度（单位体积每单位频率的能量）由下式给出：^{[4] [5]}或者，该定律可以表示为绝对温度T下频率ν的物体的光谱辐射率 ：^{[6] [7] [8]}其中，k _B是玻尔兹曼常数，h是普朗克常数，c是光在介质（无论是物质还是真空）中的速度。光谱辐射率B _ν的 cgs 单位为erg · s ⁻¹ · sr ⁻¹ · cm ⁻² · Hz ⁻¹。项B和u彼此之间有因数⁠$${\displaystyle u_{\nu }(\nu ,T)={\frac {8\pi h\nu ^{3}}{c^{3}}}{\frac {1}{\exp \left({\frac {h\nu }{k_{\mathrm {B} }T}}\right)-1}}}$$ $${\displaystyle B_{\nu }(\nu ,T)={\frac {2h\nu ^{3}}{c^{2}}}{\frac {1}{\exp \left({\frac {h\nu }{k_{\mathrm {B} }T}}\right)-1}}}$$ 4π/丙⁠因为B与方向无关，辐射以速度c传播。光谱辐射率也可以用单位波长 λ来表示，而不是用单位频率来表示。此外，该定律还可以用其他术语来表示，例如以特定波长发射的光子数量，或辐射体积中的能量密度。

在低频（即长波长）极限下，普朗克定律趋向于瑞利-金斯定律，而在高频（即小波长）极限下，它趋向于维恩近似。

马克斯·普朗克于 1900 年仅使用经验确定的常数就发展了该定律，后来他证明，以能量分布表示时，它是热力学平衡下辐射的唯一稳定分布。^[2]作为能量分布，它是热平衡分布家族中的一种，该家族包括玻色-爱因斯坦分布、费米-狄拉克分布和麦克斯韦-玻尔兹曼分布。

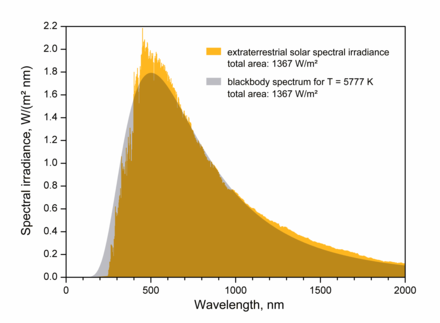
黑体是一种理想化的物体，它吸收和发射所有辐射频率。在接近热力学平衡时，发射的辐射与普朗克定律密切相关，由于它依赖于温度，普朗克辐射被称为热辐射，因此物体的温度越高，它在每个波长发射的辐射就越多。

普朗克辐射的最大强度取决于物体的温度。例如，在室温下（~300  K时，物体会发出热辐射，这些热辐射主要是红外线，不可见。在较高温度下，红外辐射量会增加，可以感觉到热量，并且会发出更多可见辐射，因此物体会发出明显的红光。在较高温度下，物体呈亮黄色或蓝白色，并发出大量短波长辐射，包括紫外线甚至X 射线。太阳表面（~6000 K）发出大量红外线和紫外线辐射；其辐射在可见光谱中达到峰值。这种因温度而引起的变化称为维恩位移定律。

普朗克辐射是任何处于热平衡状态的物体表面所能发射的最大辐射量，无论其化学成分或表面结构如何。^[9]辐射穿过介质界面的过程可以用界面的发射率（实际辐射与理论普朗克辐射之比）来表征，通常用符号ε表示。它通常取决于化学成分和物理结构、温度、波长、通过角度和极化。^[10]自然界面的发射率总是在ε = 0和 1 之间。

如果物体与另一种介质接触，且该介质的ε = 1，并吸收照射到其上的所有辐射，则该物体被称为黑体。黑体的表面可以用一个大封闭空间的壁上的小孔来模拟，该封闭空间的温度保持均匀，壁不透明，对每个波长都不是完全反射的。在平衡状态下，该封闭空间内的辐射符合普朗克定律，离开小孔的辐射也是如此。

正如麦克斯韦-玻尔兹曼分布是热平衡状态下物质粒子气体的唯一最大熵能量分布一样，普朗克分布也是光子气体的唯一最大熵能量分布。^{[11] [12]}与粒子质量和数量起作用的物质气体相比，热平衡状态下光子气体的光谱辐射度、压力和能量密度完全由温度决定。

如果光子气体不是普朗克气体，热力学第二定律保证相互作用（光子与其他粒子之间，甚至在足够高的温度下，光子本身之间的相互作用）将导致光子能量分布发生变化并接近普朗克分布。在这种接近热力学平衡的过程中，光子以正确的数量和正确的能量产生或湮灭，以普朗克分布填充腔体，直到它们达到平衡温度。就好像气体是亚气体的混合物，每个波长带都有一个亚气体，每种亚气体最终都会达到共同的温度。

B ν ( ν , T )是光谱辐射度与温度和频率的函数。在国际单位制中，它的单位是_W · m −2 · sr ⁻¹ · Hz ⁻¹。无穷^小的功率B _ν ( ν , T ) cos θ dA d Ω dν沿角度θ所描述的方向从表面法线辐射到无穷小表面面积dA 的无穷小立体角d Ω中，辐射范围为dν，中心频率为 频率。辐射到任何立体角的总功率是B _ν ( ν , T )对这三个量的积分，由斯特藩-玻尔兹曼定律给出。黑体普朗克辐射的光谱辐射度对每个偏振方向和角度都有相同的值，因此黑体被称为朗伯辐射体。

普朗克定律有多种形式，具体取决于不同科学领域的惯例和偏好。下表总结了光谱辐射定律的各种形式。左侧形式最常用于实验领域，而右侧形式最常用于理论领域。

用不同的光谱变量表示的辐射度^{[13] [14] [15] [16]}

与h		与ħ
多变的	分配	多变的	分配
频率 ν	${\displaystyle B_{\nu }(\nu ,T)={\frac {2h\nu ^{3}}{c^{2}}}{\frac {1}{e^{h\nu /( k_{\mathrm {B} }T)}-1}}}$	角频率 ω	${\displaystyle B_{\omega }(\omega ,T)={\frac {\hbar \omega ^{3}}{4\pi ^{3}c^{2}}}{\frac {1}{e^{\hbar \omega /(k_{\mathrm {B} }T)}-1}}}$
波长 λ	${\displaystyle B_{\lambda }(\lambda ,T)={\frac {2hc^{2}}{\lambda ^{5}}}{\frac {1}{e^{hc/(\lambda k_{\mathrm {B} }T)}-1}}}$	角波长 y	${\displaystyle B_{y}(y,T)={\frac {\hbar c^{2}}{4\pi ^{3}y^{5}}}{\frac {1}{e^{ \hbar c/(yk_{\mathrm {B} }T)}-1}}}$
波数 ν̃	${\displaystyle B_{\tilde {\nu }}({\tilde {\nu }},T)=2hc^{2}{\tilde {\nu }}^{3}{\frac {1}{e ^{hc{\tilde {\nu }}/(k_{\mathrm {B} }T)}-1}}}$	角波数 k	${\displaystyle B_{k}(k,T)={\frac {\hbar c^{2}k^{3}}{4\pi ^{3}}}{\frac {1}{e^{ \hbar ck/(k_{\mathrm {B} }T)}-1}}}$
分数带宽 ln x	${\displaystyle B_{\ln x}(x,T)={\frac {2k_{\mathrm {B} }^{4}T^{4}}{h^{3}c^{2}}}{\frac {x^{4}}{e^{x}-1}}}$

在分数带宽公式中，，并且积分是关于的。${\textstyle x={\frac {h\nu }{k_{\mathrm {B} }T}}={\frac {hc}{\lambda k_{\mathrm {B} }T}}}$${\textstyle \mathrm {d} (\ln x)=\mathrm {d} (\ln \nu )={\frac {\mathrm {d} \nu }{\nu }}=-{\frac {\ mathrm {d} \lambda }{\lambda }}=-\mathrm {d} (\ln \lambda )}$

普朗克定律也可以用光谱能量密度( u ) 来表示，即用B乘以⁠4π/丙⁠ : ^[17]$${\displaystyle u_{i}(T)={\frac {4\pi }{c}}B_{i}(T).}$$

用不同的光谱变量表示的光谱能量密度^[5]

与h		与ħ
多变的	分配	多变的	分配
频率 ν	${\displaystyle u_{\nu }(\nu ,T)={\frac {8\pi h\nu ^{3}}{c^{3}}}{\frac {1}{e^{h\ nu /(k_{\mathrm {B} }T)}-1}}}$	角频率 ω	${\displaystyle u_{\omega }(\omega ,T)={\frac {\hbar \omega ^{3}}{\pi ^{2}c^{3}}}{\frac {1}{e ^{\hbar \omega /(k_{\mathrm {B} }T)}-1}}}$
波长 λ	${\displaystyle u_{\lambda }(\lambda ,T)={\frac {8\pi hc}{\lambda ^{5}}}{\frac {1}{e^{hc/(\lambda k_{\mathrm {B} }T)}-1}}}$	角波长 y	${\displaystyle u_{y}(y,T)={\frac {\hbar c}{\pi ^{2}y^{5}}}{\frac {1}{e^{\hbar c/(yk_{\mathrm {B} }T)}-1}}}$
波数 ν̃	${\displaystyle u_{\tilde {\nu }}({\tilde {\nu }},T)=8\pi hc{\tilde {\nu }}^{3}{\frac {1}{e^{hc{\tilde {\nu }}/(k_{\mathrm {B} }T)}-1}}}$	角波数 k	${\displaystyle u_{k}(k,T)={\frac {\hbar ck^{3}}{\pi ^{2}}}{\frac {1}{e^{\hbar ck/(k_{\mathrm {B} }T)}-1}}}$
分数带宽 ln x	${\displaystyle u_{\ln x}(x,T)={\frac {8\pi k_{\mathrm {B} }^{4}T^{4}}{h^{3}c^{3}}}{\frac {x^{4}}{e^{x}-1}}}$

这些分布表示黑体的光谱辐射度——从发射表面发射的功率，每单位发射表面投影面积，每单位立体角，每光谱单位（频率、波长、波数或其角度等价物，或分数频率或波长）。由于辐射度是各向同性的（即与方向无关），因此以与法线成一定角度发射的功率与投影面积成正比，因此根据朗伯余弦定律，与该角度的余弦成正比，并且是非偏振的。

不同的光谱变量需要不同的相应普朗克定律表达形式。一般来说，不能简单地用一个变量代替另一个变量来转换普朗克定律的各种形式，因为这没有考虑到不同形式有不同的单位。波长和频率单位是互易的。

相应的表达形式是相关的，因为它们表达同一个物理事实：对于特定的物理光谱增量，会辐射出相应的特定的物理能量增量。

无论是用频率增量d ν来表示，还是用波长增量d λ来表示，还是用分数带宽d ν / ν或d λ / λ来表示，都是如此。引入负号可以表示频率的增量与波长的减小相对应。

为了转换相应的形式，使它们以相同的单位表达相同的量，我们乘以光谱增量。然后，对于特定的光谱增量，特定的物理能量增量可以 写成 $${\displaystyle B_{\lambda }(\lambda ,T)\,d\lambda =-B_{\nu }(\nu (\lambda ),T)\,d\nu ,}$$$${\displaystyle B_{\lambda }(\lambda ,T)=-{\frac {d\nu }{d\lambda }}B_{\nu }(\nu (\lambda ),T).}$$

另外，ν ( λ ) = ⁠丙/λ⁠，以便⁠ν/λ⁠ = − ⁠丙/λ ²⁠。代换给出了频率和波长形式之间的对应关系，以及它们不同的量纲和单位。 ^{[15] [18]} 因此， $${\displaystyle {\frac {B_{\lambda }(T)}{B_{\nu }(T)}}={\frac {c}{\lambda ^{2}}}={\frac {\nu ^{2}}{c}}.}$$

显然，普朗克定律的光谱分布峰值位置取决于光谱变量的选择。然而，从某种意义上说，根据维恩位移定律，该公式意味着光谱分布的形状与温度无关，详见下文§属性§百分位数。

分数带宽形式与其他形式有如下关系^[16]

${\displaystyle B_{\ln x}=\nu B_{\nu }=\lambda B_{\lambda }}$。

在上述普朗克定律的变体中，波长和波数变体使用项2 hc ²和⁠碳/千_​⁠仅由物理常数组成。因此，这些项可以被视为物理常数本身， ^[19]因此被称为第一辐射常数 c _{1 L}和第二辐射 常数 c ₂

和

利用辐射常数，普朗克定律的 波长变体可以简化为 ，波数变体也可以相应地简化。 $${\displaystyle L(\lambda ,T)={\frac {c_{1L}}{\lambda ^{5}}}{\frac {1}{\exp \left({\frac {c_{2}}{\lambda T}}\right)-1}}}$$

这里使用L代替B，因为它是光谱辐射度的 SI 符号。c 1 _L中的L指的是 L。这个引用是必要的，因为普朗克定律可以重新表述为光谱辐射出射度_M ( λ , T )而不是光谱辐射度L ( λ , T )，在这种情况下， c ₁替换c _{1 L}，其中

因此，普朗克光谱辐射出射定律可以写成 $${\displaystyle M(\lambda ,T)={\frac {c_{1}}{\lambda ^{5}}}{\frac {1}{\exp \left({\frac {c_{2}}{\lambda T}}\right)-1}}}$$

随着测量技术的进步，国际计量大会修改了对c ₂的估算；详情 请参阅普朗克轨迹 § 国际温标。

普朗克定律描述了热力学平衡下电磁辐射的独特特征光谱分布，此时没有物质或能量的净流动。^[2]通过考虑具有刚性不透明壁的腔体中的辐射，最容易理解其物理原理。 壁的运动会影响辐射。 如果壁不是不透明的，那么热力学平衡就不是孤立的。 解释如何达到热力学平衡是很有意义的。 主要有两种情况： (a) 当接近热力学平衡时存在物质，即腔壁对每个波长的反射都不完全，或者腔壁完全反射而腔内有一个小黑体（这是普朗克考虑的主要情况）；或 (b) 当接近平衡时没有物质，即腔壁对所有波长的反射都是完全的，而腔体中不含有物质。 对于未封闭在这种腔中的物质，可以通过适当运用普朗克定律来近似解释热辐射。

经典物理学通过能量均分定理，预测黑体辐射总强度为无限大 ，从而导致紫外灾变。如果加上经典上无法证明的假设 ，即由于某种原因辐射是有限的 ，经典热力学可以解释普朗克分布的某些方面 ，如斯特藩-玻尔兹曼定律和维恩位移定律。对于物质存在的情况 ，量子力学提供了很好的解释 ，如下面“爱因斯坦系数”一节所述 。这是爱因斯坦考虑过的情况 ，如今用于量子光学 。^{[20] [21]}对于没有物质的情况 ，量子场论是必要的 ，因为具有固定粒子数的非相对论量子力学无法提供充分的解释。

普朗克定律的量子理论解释将辐射视为处于热力学平衡状态的无质量、不带电的玻色子粒子（即光子）气体。光子被视为带电基本粒子之间电磁相互作用的载体。光子数不守恒。光子以正确的数量和正确的能量产生或湮灭，以普朗克分布填充腔体。对于处于热力学平衡状态的光子气体，内部能量密度完全由温度决定；此外，压力完全由内部能量密度决定。这与物质气体的热力学平衡情况不同，物质气体的内部能量不仅由温度决定，还独立地由不同分子的各自数量决定，并且再次独立地由不同分子的具体特性决定。对于给定温度下的不同物质气体，压力和内部能量密度可以独立变化，因为不同的分子可以独立地携带不同的激发能量。

普朗克定律是玻色-爱因斯坦分布的一个极限，该分布是一种描述热力学平衡下无相互作用玻色子的能量分布。对于光子和胶子等无质量玻色子，化学势为零，玻色-爱因斯坦分布简化为普朗克分布。还有另一种基本的平衡能量分布：费米-狄拉克分布，它描述热平衡下的费米子，比如电子。这两个分布的不同之处在于，多个玻色子可以占据相同的量子态，而多个费米子则不能。在低密度下，每个粒子可用的量子态数量很大，这种差异变得无关紧要。在低密度极限下，玻色-爱因斯坦和费米-狄拉克分布均简化为麦克斯韦-玻尔兹曼分布。

基尔霍夫热辐射定律是对复杂物理情况的简洁而简短的描述。以下是对这种情况的介绍性概述，远非严格的物理论证。这里的目的只是总结这种情况中的主要物理因素和主要结论。

传导热传递和辐射热传递之间存在差异。辐射热传递可以通过过滤，只允许特定波段的辐射频率通过。

众所周知，物体越热，其在每个频率上辐射的热量就越多。

在一个不透明体腔体中，腔壁坚固且在任何频率下都无法完美反射，在热力学平衡状态下，只有一个温度，并且每个频率的辐射都必须共享这个温度。

我们可以想象两个这样的腔体，每个腔体都处于各自独立的辐射和热力学平衡状态。我们可以想象一个光学装置，它允许两个腔体之间进行辐射热传递，经过滤波后只允许一定范围的辐射频带通过。如果腔体中辐射的光谱辐射度值在该频带上有所不同，那么热量就会从较热的部分流向较冷的部分。我们可以提议在这样的频带内使用这种滤波传热来驱动热机。如果两个物体的温度相同，则热力学第二定律不允许热机工作。可以推断，对于两个物体共同的温度，通带内的光谱辐射度值也必须是共同的。这对于每个频带都必须成立。^{[22] [23] [24]}巴尔弗·斯图尔特 (Balfour Stewart) 和后来的基尔霍夫 (Kirchhoff) 都清楚地认识到了这一点。巴尔弗·斯图尔特 (Balfour Stewart) 通过实验发现，在所有表面中，通过各种过滤器判断，无论何种辐射质量，烟黑表面发出的热辐射量都是最大的。

基尔霍夫从理论上进一步思考，指出这意味着，任何处于热力学平衡状态的空腔的光谱辐射率（作为辐射频率的函数）必定是温度的唯一通用函数。他假设一个理想的黑体，它与周围环境的接触方式恰好可以吸收落在其上的所有辐射。根据亥姆霍兹互易原理，来自这种物体内部的辐射将不受阻碍地直接传递到其周围环境，而不会在界面处发生反射。在热力学平衡状态下，从这种物体发出的热辐射将具有作为温度函数的唯一通用光谱辐射率。这一见解是基尔霍夫热辐射定律的根源。

可以想象一个标记为X且温度为T _{X 的}小的均匀球形材料体位于一个大空腔内的辐射场中，空腔壁为标记为Y且温度为T _Y的材料。物体X发射自己的热辐射。在特定频率ν下，从特定横截面沿某一方向通过X中心发射的辐射，该方向垂直于该横截面，可以表示为I _{ν , X} ( T _X ) ，这是X材料的特性。在该频率ν下，从壁面沿相反方向进入该横截面的辐射功率，对于壁面温度T _Y ，可以表示为I _{ν , Y} ( T _Y )。对于材料X，定义吸收率α _{ν , X , Y} ( T _X , T _Y )为入射辐射被X吸收的部分，即入射能量以α _{ν , X , Y} ( T _X , T _Y ) I _{ν , Y} ( T _Y )的速率被吸收。

能量在某种意义上积累到身体横截面的 速率q ( ν , T _X , T _Y )可以表示为$${\displaystyle q(\nu ,T_{X},T_{Y})=\alpha _{\nu ,X,Y}(T_{X},T_{Y})I_{\nu ,Y}(T_{Y})-I_{\nu ,X}(T_{X}).}$$

上文中提到，基尔霍夫的开创性见解是，在温度T 的热力学平衡下，存在一个独特的宇宙辐射分布，现称为B _ν ( T )，它与材料X和Y的化学特性无关，这有助于我们理解任何物体的辐射交换平衡，如下所示。

当温度为T时达到热力学平衡时，腔壁发出的辐射具有唯一的普适值，即I _{ν , Y} ( T _Y ) = B _ν ( T )。此外，还可定义物体X的材料的发射率ε _{ν , X} ( T _X )，使得在温度为T _X = T 的热力学平衡下，有I _{ν , X} ( T _X ) = I _{ν , X} ( T ) = ε _{ν , X} ( T ) B _ν ( T )。

当温度为T = T _X = T _Y时，热平衡占主导地位，能量积累率消失，因此q ( ν , T _X , T _Y ) = 0。因此，在热力学平衡中，当T = T _X = T _Y时， $${\displaystyle 0=\alpha _{\nu ,X,Y}(T,T)B_{\nu }(T)-\epsilon _{\nu ,X}(T)B_{\nu }(T).}$$

基尔霍夫指出，在热力学平衡状态下，当T = T _X = T _Y时， $${\displaystyle \alpha _{\nu ,X,Y}(T,T)=\epsilon _{\nu ,X}(T).}$$

引入特殊符号α _{ν , X} ( T )来表示材料X在温度T时的热力学平衡时的吸收率（由爱因斯坦的发现证明，如下所示），进一步得到 热力学平衡时的 等式 。$${\displaystyle \alpha _{\nu ,X}(T)=\epsilon _{\nu ,X}(T)}$$

这里展示的吸收率和发射率相等是温度T时热力学平衡所特有的，当热力学平衡条件不成立时，一般不会期望这种相等。发射率和吸收率是材料分子的各自属性，但由于爱因斯坦发现的一种称为“受激发射”的现象，它们对分子激发状态分布的依赖程度不同。当材料处于热力学平衡或称为局部热力学平衡的状态时，发射率和吸收率会相等。非常强的入射辐射或其他因素会破坏热力学平衡或局部热力学平衡。气体中的局部热力学平衡意味着在确定分子激发状态分布时，分子碰撞远远超过光发射和吸收。

基尔霍夫指出，他不知道 B _ν ( T )的精确特征，但他认为找出这一特征很重要。在基尔霍夫洞察其存在和特征的一般原理四十年后，普朗克的贡献是确定了平衡分布B _ν ( T )的精确数学表达式。

在物理学中，人们认为理想的黑体（这里标记为B）是指能够完全吸收落在其上的所有频率ν的电磁辐射的黑体（因此称为“黑体”）。根据基尔霍夫热辐射定律，这意味着，对于每个频率ν，在温度T 的热力学平衡下，都有α _ν，B ( T ) = ε _ν，B ( T ) = 1，因此黑体的热辐射量始终等于普朗克定律规定的总量。没有物理物体能够发射超过黑体的热辐射量，因为如果它与辐射场处于平衡状态，它发射的能量将大于入射到它身上的能量。

虽然不存在完全黑色的材料，但实际上可以精确地近似黑色表面。^[2]至于其材料内部，如果凝聚态物质、液体、固体或等离子体与周围环境有明确的界面，则如果完全不透明，则对辐射而言是完全黑色的。这意味着它会吸收所有穿透物体与周围环境界面并进入物体的辐射。这在实践中并不难实现。另一方面，自然界中不存在完全黑色的界面。完全黑色的界面不会反射任何辐射，但会传输落在其两侧的所有辐射。制作有效黑色界面的最佳实用方法是通过完全不透明的刚性材料体中大腔壁上的小孔来模拟“界面”，该材料在任何频率下都不会完全反射，其壁处于受控温度。除了这些要求之外，壁的组成材料不受限制。进入小孔的辐射几乎没有可能在不与壁多次撞击的情况下逃逸出腔体。^[25]

普朗克曾解释道^[26] ，辐射体的内部由物质组成，它与相邻的物质介质之间存在界面，而该介质通常是从内部观察辐射体的介质。界面不是由物理物质构成，而是一个理论概念，一个数学上的二维表面，是两个相邻介质的联合属性，严格来说不属于任何一个单独介质。这样的界面既不能吸收也不能发射，因为它不是由物理物质构成的；但它是辐射反射和透射的场所，因为它是一个光学特性不连续的表面。界面处辐射的反射和透射遵循斯托克斯-亥姆霍兹互易原理。

在温度为T时处于热力学平衡状态的空腔内，黑体内部的任何一点的辐射都是均匀、各向同性的和非偏振的。黑体吸收所有入射到其上的电磁辐射，不反射任何入射到其上的电磁辐射。根据亥姆霍兹互易原理，来自黑体内部的辐射不会在其表面反射，而是完全传输到其外部。由于黑体内部辐射的各向同性，从其内部通过其表面传输到其外部的辐射的光谱辐射度与方向无关。^[27]

可以这样表达：处于热力学平衡状态的黑体表面辐射遵循朗伯余弦定律。^{[28] [29]}这意味着，从黑体实际发射表面的给定面积为dA的无穷小元素（该元素与黑体在 dA 处的法线成 θ 角）检测到的光谱通量d Φ（dA，θ，dΩ，dν）进入以θ所示方向为中心的立体检测角为dΩ的元素（在频带宽度为dν的元素中），可表示为^[30] 其中，L ⁰（dA，dν）表示如果沿法线方向θ = 0测量，面积dA将显示的每单位面积、每单位频率、每单位立体角的通量。 $${\displaystyle {\frac {d\Phi (dA,\theta ,d\Omega ,d\nu )}{d\Omega }}=L^{0}(dA,d\nu )\,dA\,d\nu \,\cos \theta }$$

存在因子cos θ是因为光谱辐射直接指代的面积是实际发射表面面积在垂直于θ方向的平面上的投影。这就是余弦定律名称的由来。

考虑到热力学平衡状态下黑体表面辐射光谱辐射度的方向独立性，有L ⁰ ( dA , dν ) = B _ν ( T )，因此 $${\displaystyle {\frac {d\Phi (dA,\theta ,d\Omega ,d\nu )}{d\Omega }}=B_{\nu }(T)\,dA\,d\nu \,\cos \theta .}$$

因此，朗伯余弦定律表达了热力学平衡状态下黑体表面 光谱辐射亮度B _ν ( T )的方向独立性。

通过对根据朗伯定律得出的黑体谱通量在所有频率上以及与黑体表面上方半球 ( h ) 对应的立体角 上进行积分，可以找到黑体表面每单位面积发射的总功率 ( P )。$${\displaystyle P=\int _{0}^{\infty }d\nu \int _{h}d\Omega \,B_{\nu }\cos(\theta )}$$

无穷小立体角可以用球极坐标表示： 因此： 其中称为斯特藩-玻尔兹曼常数。^[31]$${\displaystyle d\Omega =\sin(\theta )\,d\theta \,d\phi .}$$$${\displaystyle P=\int _{0}^{\infty }d\nu \int _{0}^{\tfrac {\pi }{2}}d\theta \int _{0}^{2\pi }d\phi \,B_{\nu }(T)\cos(\theta )\sin(\theta )=\sigma T^{4}}$$$${\displaystyle \sigma ={\frac {2k_{\mathrm {B} }^{4}\pi ^{5}}{15c^{2}h^{3}}}\approx 5.670400\times 10^{-8}\,\mathrm {J\,s^{-1}m^{-2}K^{-4}} }$$

辐射传输方程描述了辐射在穿过物质介质时受到的影响。对于物质介质在介质中某点附近处于热力学平衡的特殊情况，普朗克定律具有特殊重要性。

为简单起见，我们可以考虑线性稳定状态，没有散射。辐射传输方程表明，对于穿过短距离d s的光束，能量守恒：该光束的（光谱）辐射度变化（ I _ν）等于材料介质去除的量加上从材料介质获得的量。如果辐射场与材料介质处于平衡状态，则这两个贡献将相等。材料介质将具有一定的发射系数和吸收系数。

吸收系数α是光束在传播距离d s时强度的分数变化，单位为长度⁻¹。它由两部分组成，一部分是由于吸收而引起的强度减小，另一部分是由于受激发射而引起的强度增加。受激发射是由入射辐射引起的，并且与入射辐射成正比。它被包括在吸收项中，因为与吸收一样，它与入射辐射的强度成正比。由于吸收量通常会随着材料密度ρ线性变化，我们可以定义“质量吸收系数” κ _ν = ⁠α/ρ⁠这是材料本身的属性。当光束穿过一小段距离d s时，由于吸收而导致的强度变化将是^[7] $${\displaystyle dI_{\nu }=-\kappa _{\nu }\rho I_{\nu }\,ds}$$

“质量发射系数” j _ν等于小体积元素每单位体积的辐射率除以其质量（因为与质量吸收系数一样，发射率与发射质量成正比），单位为功率⋅立体角^−1⋅频率^−1⋅密度⁻¹。与质量吸收系数一样，它也是材料本身的属性。光束在穿过一小段距离d s时的变化将是^[32] $${\displaystyle dI_{\nu }=j_{\nu }\rho \,ds}$$

辐射传输方程将是这两个贡献的总和：^[33] $${\displaystyle {\frac {dI_{\nu }}{ds}}=j_{\nu }\rho -\kappa _{\nu }\rho I_{\nu }.}$$

如果辐射场与物质介质处于平衡状态，则辐射将是均匀的（与位置无关），因此dI _ν = 0且： 这是基尔霍夫定律的另一种表述，将介质的两种物质性质联系起来，并得出介质在热力学平衡点附近的辐射传输方程： $${\displaystyle \kappa _{\nu }B_{\nu }=j_{\nu }}$$$${\displaystyle {\frac {dI_{\nu }}{ds}}=\kappa _{\nu }\rho (B_{\nu }-I_{\nu }).}$$

详细平衡原理指出，在热力学平衡下，每个基本过程都通过其逆过程来平衡。

1916 年，阿尔伯特·爱因斯坦将这一原理应用于原子层面，研究原子在两个特定能级之间跃迁而辐射和吸收辐射的情况，^{[34]从而更深入地了解了这种辐射的辐射传输方程和基尔霍夫定律。 如果能级 1 是能量为}E _{1 的}较低能级，能级 2 是能量为E _{2 的}较高能级，则辐射或吸收的辐射频率ν将由玻尔频率条件确定：^{[35] [36]} $${\displaystyle E_{2}-E_{1}=h\nu .}$$

如果n ₁和n ₂分别是状态 1 和 2 下原子的数密度，则这些密度随时间的变化率将归因于三个过程：

自发辐射

${\displaystyle \left({\frac {dn_{1}}{dt}}\right)_{\mathrm {spon} }=A_{21}n_{2}}$

受激发射

${\displaystyle \left({\frac {dn_{1}}{dt}}\right)_{\mathrm {stim} }=B_{21}n_{2}u_{\nu }}$

光吸收

${\displaystyle \left({\frac {dn_{2}}{dt}}\right)_{\mathrm {abs} }=B_{12}n_{1}u_{\nu }}$

其中u _ν是辐射场的光谱能量密度。三个参数A ₂₁、B ₂₁和B ₁₂称为爱因斯坦系数，与两个能级（状态）之间跃迁产生的光子频率ν相关。因此，光谱中的每条线都有一组相关的系数。当原子和辐射场处于平衡状态时，辐射亮度将由普朗克定律给出，根据详细平衡原理，这些速率之和必须为零： $${\displaystyle 0=A_{21}n_{2}+B_{21}n_{2}{\frac {4\pi }{c}}B_{\nu }(T)-B_{12}n_{1}{\frac {4\pi }{c}}B_{\nu }(T)}$$

由于原子也处于平衡状态，因此两个能级的粒子数由玻尔兹曼因子关联： 其中g ₁和g ₂是各自能级的多重性。将上述两个方程与它们在任何温度下都有效的要求结合起来，可以得到爱因斯坦系数之间的两个关系： 因此，知道一个系数就可以知道另外两个系数。 $${\displaystyle {\frac {n_{2}}{n_{1}}}={\frac {g_{2}}{g_{1}}}e^{-h\nu /k_{\mathrm {B} }T}}$$$${\displaystyle {\frac {A_{21}}{B_{21}}}={\frac {8\pi h\nu ^{3}}{c^{3}}}}$$ $${\displaystyle {\frac {B_{21}}{B_{12}}}={\frac {g_{1}}{g_{2}}}}$$

对于各向同性的吸收和发射情况，上文辐射传输部分中定义的发射系数 ( j _ν ) 和吸收系数 ( κ _ν ) 可以用爱因斯坦系数来表示。爱因斯坦系数之间的关系将产生上文辐射传输部分中表达的基尔霍夫定律的表达式，即$${\displaystyle j_{\nu }=\kappa _{\nu }B_{\nu }.}$$

这些系数适用于原子和分子。

分布B _ν、B _ω、B _ν̃和B _k在光子能量为^[37]时达到峰值，其中W是朗伯W函数，e是欧拉数。 $${\displaystyle E=\left[3+W\left(-3e^{-3}\right)\right]k_{\mathrm {B} }T\approx 2.821\ k_{\mathrm {B} }T,}$$

然而，分布B _{λ 的}峰值在不同的能量处^[37]出现这种情况的原因是，如上所述，不能简单地通过将ν替换为λ而从（例如） B _ν变为B _λ。此外，还必须乘以，这会将分布的峰值移向更高的能量。当分别使用相等大小的频率或波长箱进行分组时，这些峰值是光子的模式能量。将hc ($${\displaystyle E=\left[5+W\left(-5e^{-5}\right)\right]k_{\mathrm {B} }T\approx 4.965\ k_{\mathrm {B} }T,}$$${\textstyle \left|{d\nu }/{d\lambda }\right|=c/{\lambda ^{2}}}$14 387 .770 μm·K )，通过这些能量表达式给出了峰值的波长。

这些峰值的光谱辐射度由下式给出：

${\displaystyle {\begin{aligned}B_{\nu ,{\text{max}}}(T)&={\frac {2k_{\mathrm {B} }^{3}T^{3}x^{3}}{h^{2}c^{2}}}{\frac {1}{e^{x}-1}}\\&\approx 1.896\times 10^{-19}{\frac {\mathrm {W} }{\mathrm {m^{2}\cdot Hz\cdot sr} }}\times (T/\mathrm {K} )^{3}\\\end{aligned}}}$

与和与${\displaystyle x=3+W(-3e^{-3}),}$$${\displaystyle {\begin{aligned}B_{\lambda ,{\text{max}}}(T)&={\frac {2k_{\mathrm {B} }^{5}T^{5}x^{5}}{h^{4}c^{3}}}{\frac {1}{e^{x}-1}}\\&\approx 4.096\times 10^{-6}{\frac {\text{W}}{{\text{m}}^{2}\cdot {\text{sr}}}}\times ~(T/{\text{K}})^{5}\end{aligned}}}$$${\displaystyle x=5+W(-5e^{-5}).}$

同时，来自黑体的光子的平均能量为，其中是黎曼zeta函数。 $${\displaystyle E=\left[{\frac {\pi ^{4}}{30\ \zeta (3)}}\right]k_{\mathrm {B} }T\approx 2.701\ k_{\mathrm {B} }T,}$$${\displaystyle \zeta }$

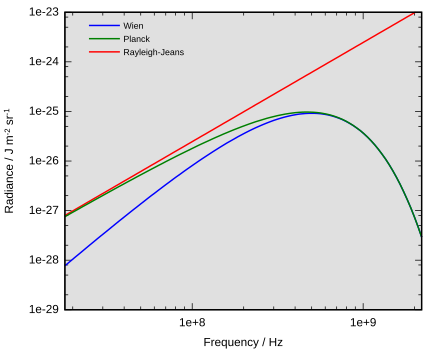
在低频（即长波长）极限下，普朗克定律变为瑞利-金斯定律^{[38] [39] [40]} 或 $${\displaystyle B_{\nu }(T)\approx {\frac {2\nu ^{2}}{c^{2}}}k_{\mathrm {B} }T}$$$${\displaystyle B_{\lambda }(T)\approx {\frac {2c}{\lambda ^{4}}}k_{\mathrm {B} }T}$$

辐射亮度随频率的平方而增加，说明了紫外线灾变。在高频（即小波长）极限下，普朗克定律趋向于维恩近似：^{[40] [41] [42]} 或$${\displaystyle B_{\nu }(T)\approx {\frac {2h\nu ^{3}}{c^{2}}}e^{-{\frac {h\nu }{k_{\mathrm {B} }T}}}}$$$${\displaystyle B_{\lambda }(T)\approx {\frac {2hc^{2}}{\lambda ^{5}}}e^{-{\frac {hc}{\lambda k_{\mathrm {B} }T}}}.}$$

百分位数	λ T (微米·开尔文)	λkBT / hc​​​
0.01%	910	0.0632
0.1％	1110	0.0771
1％	1448	0.1006
10％	2195	0.1526
20％	2676	0.1860
25.0％	2898	0.2014
30％	3119	0.2168
40％	3582	0.2490
41.8％	3670	0.2551
50％	4107	0.2855
60％	4745	0.3298
64.6%	5099	0.3544
70％	5590	0.3885
80％	6864	0.4771
90％	9376	0.6517
99％	22884	1.5905
99.9％	51613	3.5873
99.99％	113374	7.8799

维恩位移定律的强形式表明，普朗克定律的形状与温度无关。因此，可以列出总辐射的百分位点以及波长和频率的峰值，其形式为波长λ除以温度T。^[43]下表第二列列出了λT的对应值，即波长λ为 的x值。十/电视⁠ 第一列中相应条目给出的辐射百分位点 的微米。

也就是说，0.01% 的辐射波长低于⁠910/电视⁠  μm，20% 以下⁠2676/电视⁠ μm等。波长和频率峰值以粗体显示，分别出现在 25.0% 和 64.6% 处。41.8% 点是波长频率中性峰值（即波长或频率对数每单位变化的功率峰值）。这些是各自普朗克定律发挥作用的点⁠1/λ ⁵⁠ , ν ³和⁠ν2^​/λ ²⁠分别除以exp ( ⁠ν/KBT_​​⁠ ) − 1达到最大值。波长比率在 0.1% 和 0.01% 之间（1110 比 910 多 22%）比在 99.9% 和 99.99% 之间（113374 比 51613 多 120%）的差距要小得多，这反映了短波长（左端）能量呈指数衰减，长波长呈多项式衰减。

使用哪个峰值取决于应用。常规选择是弱形式的维恩位移定律给出的 25.0% 处的波长峰值。对于某些目的，将总辐射分成两半的中值或 50% 点可能更合适。后者更接近频率峰值而不是波长峰值，因为辐射在短波长下呈指数下降，而在长波长下仅呈多项式下降。出于同样的原因，中性峰出现在比中值更短的波长处。

百分位数	太阳λ (微米) [44]	5778K 时的黑体	288 K行星λ（微米）
0.01%	0.203	0.157	3.16
0.1％	0.235	0.192	3.85
1％	0.296	0.251	5.03
10％	0.415	0.380	7.62
20％	0.484	0.463	9.29
25.0％	0.520	0.502	10.1
30％	0.556	.540	10.8
41.8％	0.650	0.635	12.7
50％	0.727	0.711	14.3
60％	0.844	0.821	16.5
64.6%	0.911	0.882	17.7
70％	1.003	0.967	19.4
80％	1.242	1.188	23.8
90％	1.666	1.623	32.6
99％	3.728	3.961	79.5
99.9％	8.208	8.933	179
99.99％	17.548	19.620	394

太阳辐射可与约 5778 K 的黑体辐射进行比较（但请参见图表）。右侧表格显示了此温度下黑体的辐射如何划分，以及阳光如何划分以供比较。为了进行比较，还显示了一个以黑体为模型的行星，其辐射温度为标称 288 K（15 °C），这是地球高度变化的温度的代表值。其波长是太阳波长的二十多倍，以微米（数千纳米）为单位列在第三列中。

也就是说，只有 1% 的太阳辐射波长短于 296 nm，只有 1% 的太阳辐射波长长于 3728 nm。以微米表示，98% 的太阳辐射波长范围为 0.296 至 3.728 μm。288 K 行星辐射的相应 98% 能量波长范围为 5.03 至 79.5 μm，远高于太阳辐射范围（如果以频率ν =表示，则低于该范围）丙/λ⁠而不是波长λ）。

由于太阳辐射和行星辐射的波长相差超过一个数量级，因此设计用于让其中一种通过并阻挡另一种的滤光片很容易制造。例如，用普通玻璃或透明塑料制成的窗户至少可以让 80% 的入射 5778 K 太阳辐射（波长低于 1.2 μm）通过，同时阻挡 99% 以上的 288 K 热辐射（波长 5 μm 以上），而大多数建筑级厚度的玻璃和塑料在此波长下实际上是不透明的。

太阳辐射到达大气层顶部 (TOA) 时，即为太阳辐射。从表中可以看出，波长低于 400 nm 的辐射（即紫外线）约占 8%，波长高于 700 nm 的辐射（即红外线）约占 48%，占总辐射的 52%。因此，只有 40% 的 TOA 日照量是人眼可见的。大气层吸收了大部分紫外线和大量红外线，因此使这些百分比大幅偏向可见光。

考虑一个边长为L的立方体，其壁面导电，内充满电磁辐射，温度为T ，处于热平衡状态。如果其中一个壁面上有一个小孔，则从小孔发射的辐射将具有完美黑体的特征。我们将首先计算腔内的光谱能量密度，然后确定发射辐射的光谱辐射度。

在立方体的壁上，电场的平行分量和磁场的正交分量必须消失。与盒子中粒子的波函数类似，人们发现场是周期函数的叠加。在与壁正交的三个方向上的三个波长λ ₁、λ ₂和λ ₃可以是：其中n _i是正整数。对于每一组整数n _{i ，}都有两个线性独立的解（称为模式）。每组整数n _i的两个模式对应于自旋为 1 的光子的两个偏振态。根据量子理论，一个模式的总能量由下式给出： $${\displaystyle \lambda _{i}={\frac {2L}{n_{i}}},}$$

${\displaystyle E_{n_{1},n_{2},n_{3}}\left(r\right)=\left(r+{\frac {1}{2}}\right){\frac {hc}{2L}}{\sqrt {n_{1}^{2}+n_{2}^{2}+n_{3}^{2}}}.}$

1

数字r可以解释为模式中的光子数。当r = 0时，模式的能量不为零。电磁场的真空能量是卡西米尔效应的原因。下面我们将计算绝对温度 T下的盒子内部能量。

根据统计力学，特定模式能级的平衡概率分布由下式给出：其中我们使用温度倒数分母Z ( β )是单个模式的配分函数。它使P _r正确归一化，并可以如下 方式评估$${\displaystyle P_{r}={\frac {e^{-\beta E\left(r\right)}}{Z\left(\beta \right)}}.}$$$${\displaystyle \beta \ {\stackrel {\mathrm {def} }{=}}\ {\frac {1}{k_{\mathrm {B} }T}}.}$$$${\displaystyle Z\left(\beta \right)=\sum _{r=0}^{\infty }e^{-\beta E\left(r\right)}={\frac {e^{-\beta \varepsilon /2}}{1-e^{-\beta \varepsilon }}},}$$

${\displaystyle \varepsilon ={\frac {hc}{2L}}{\sqrt {n_{1}^{2}+n_{2}^{2}+n_{3}^{2}}}.}$

2

是单个光子的能量。模式中的平均能量可以通过配分函数得到：除了第一个真空能量项外，该公式是服从玻色-爱因斯坦统计的粒子一般公式的一个特例。由于对光子总数没有限制，因此化学势为零。 $${\displaystyle \left\langle E\right\rangle =-{\frac {d\log \left(Z\right)}{d\beta }}={\frac {\varepsilon }{2}}+{\frac {\varepsilon }{e^{\beta \varepsilon }-1}}.}$$

如果我们测量相对于基态的能量，盒子里的总能量如下：ε/2⁠在所有允许的单光子态上。当L趋近于无穷大时，这可以在热力学极限下精确地完成。在这个极限下， ε变为连续的，然后我们可以积分⟨ E ⟩ − ⁠ε/2⁠超过此参数。要以这种方式计算盒子中的能量，我们需要评估给定能量范围内有多少个光子状态。如果我们将能量介于ε和ε + dε之间的单光子状态总数写为g ( ε ) dε，其中g ( ε )是状态密度（下面将进行评估），则总能量由下式给出

${\displaystyle U=\int _{0}^{\infty }{\frac {\varepsilon }{e^{\beta \varepsilon }-1}}g(\varepsilon )\,d\varepsilon .}$

3

为了计算态密度，我们将方程 ( 2 ) 重写如下：其中n是向量n = ( n ₁ , n ₂ , n ₃ )的范数。 $${\displaystyle \varepsilon \ {=}\ {\frac {hc}{2L}}n,}$$

对于每个具有大于或等于零的整数分量的矢量n ，有两个光子状态。这意味着n空间中某个区域中的光子状态数量是该区域体积的两倍。能量范围dε对应于厚度为dn =的壳层⁠2升/碳⁠ n空间中的d ε 。因为n的分量必须为正，所以这个壳跨越了球体的八分之一。在能量范围dε内，光子态g ( ε ) dε的数量由以下公式给出：将其代入等式 ( 3 ) 并除以体积V = L ³可得出总能量密度其中频率相关的光谱能量密度u _ν ( T )由以下公式给出由于辐射在所有方向上都是相同的，并且以光速传播，所以离开小孔的辐射的光谱辐射率为 由此得出普朗克定律通过改变总能量积分中的变量，可以得到该定律的其他形式。以上推导基于 Brehm & Mullin 1989。 $${\displaystyle g(\varepsilon )\,d\varepsilon =2{\frac {1}{8}}4\pi n^{2}\,dn={\frac {8\pi L^{3}}{h^{3}c^{3}}}\varepsilon ^{2}\,d\varepsilon .}$$$${\displaystyle {\frac {U}{V}}=\int _{0}^{\infty }u_{\nu }(T)\,d\nu ,}$$$${\displaystyle u_{\nu }(T)={8\pi h\nu ^{3} \over c^{3}}{1 \over e^{h\nu /k_{\mathrm {B} }T}-1}.}$$$${\displaystyle B_{\nu }(T)={\frac {u_{\nu }(T)c}{4\pi }},}$$$${\displaystyle B_{\nu }(T)={\frac {2h\nu ^{3}}{c^{2}}}~{\frac {1}{e^{h\nu /k_{\mathrm {B} }T}-1}}.}$$

对于非简并情况，A 和 B 系数可以使用量子力学中时间相关微扰理论中的偶极子近似来计算。计算 A 也需要二次量化，因为半经典理论无法解释自发辐射，因为自发辐射不会随着扰动场趋于零而趋于零。因此计算出的跃迁率为（以 SI 单位为单位）：^{[45] [46] [47]}

${\displaystyle w_{i\rightarrow f}^{s.emi}={\frac {\omega _{if}^{3}e^{2}}{3\pi \epsilon _{0}\hbar c^{3}}}|\langle f|{\vec {r}}|i\rangle |^{2}=A_{if}}$

${\displaystyle w_{i\rightarrow f}^{abs}={\frac {u(\omega _{fi})\pi e^{2}}{3\epsilon _{0}\hbar ^{2}}}|\langle f|{\vec {r}}|i\rangle |^{2}=B_{if}^{abs}u(\omega _{fi})}$

${\displaystyle w_{i\rightarrow f}^{emi}={\frac {u(\omega _{if})\pi e^{2}}{3\epsilon _{0}\hbar ^{2}}}|\langle f|{\vec {r}}|i\rangle |^{2}=B_{if}^{emi}u(\omega _{if})}$

注意，跃迁速率公式取决于偶极矩算子。对于高阶近似，它涉及四极矩和其他类似项。因此，A 和 B 系数（对应于角频率能量分布）为：

${\displaystyle A_{ab}={\frac {\omega _{ab}^{3}e^{2}}{3\pi \epsilon _{0}\hbar c^{3}}}|\langle a|{\vec {r}}|b\rangle |^{2}}$

${\displaystyle B_{ab}={\frac {\pi e^{2}}{3\epsilon _{0}\hbar ^{2}}}|\langle a|{\vec {r}}|b\rangle |^{2}}$

其中，对于非退化情况，系数 A 和 B 满足给定的比率： ${\displaystyle \omega _{ab}={\frac {E_{a}-E_{b}}{\hbar }}}$

${\displaystyle {\frac {B_{12}}{B_{21}}}=1}$和 。${\displaystyle {\frac {A_{if}}{B}}={\frac {\omega _{if}^{3}\hbar }{\pi ^{2}c^{3}}}}$

另一个有用的比率是麦克斯韦分布，它表明能级中的粒子数与的指数成正比。从数学上讲： ${\displaystyle E}$${\displaystyle \beta E}$

${\displaystyle {\frac {N_{a}}{N_{b}}}={\frac {e^{-E_{a}\beta }}{e^{-E_{b}\beta }}}=e^{\omega _{ba}\hbar \beta }}$

其中和分别是和 的占据能级数，其中。然后，使用：${\displaystyle N_{a}}$${\displaystyle N_{b}}$${\displaystyle E_{a}}$${\displaystyle E_{b}}$${\displaystyle E_{b}>E_{a}}$${\displaystyle {\frac {dN_{b}}{dt}}=-A_{ba}N_{b}-N_{b}u(\omega _{ba})B_{ba}+N_{a}u(\omega _{ba})B_{ab}=-N_{b}w_{b\rightarrow a}^{s.emi}-N_{b}w_{b\rightarrow a}^{emi}+N_{a}w_{a\rightarrow b}^{abs}}$

求解平衡条件，并利用导出的比率，我们得到普朗克定律： ${\displaystyle u}$${\displaystyle {\frac {dN_{b}}{dt}}=0}$

${\displaystyle u_{\omega }(\omega ,T)={\frac {\omega ^{3}\hbar }{\pi ^{2}c^{3}}}{\frac {1}{e^{\omega \hbar \beta }-1}}}$。

1858 年，巴尔弗·斯图尔特 (Balfour Stewart)描述了他对各种物质的抛光板的热辐射发射和吸收能力的实验，并与相同温度下的烟黑表面进行了比较。 ^[9]斯图尔特之所以选择烟黑表面作为参考，是因为之前有各种实验结果，尤其是皮埃尔·普雷沃斯特 (Pierre Prevost)和约翰·莱斯利 (John Leslie)的实验结果。他写道：“烟黑吸收了落在其上的所有光线，因此具有最大的吸收能力，也将具有最大的辐射能力。”

斯图尔特用热电堆和用显微镜读取的灵敏检流计测量辐射功率。他关注的是选择性热辐射，他用一盘物质研究了选择性辐射和吸收不同辐射质量的物质，而不是最大限度地吸收所有辐射质量的物质。他从可以反射和折射的射线的角度讨论了实验，这些射线遵循亥姆霍兹互易原理（尽管他没有用同名术语来称呼它）。他在这篇论文中没有提到射线的质量可以用它们的波长来描述，也没有使用棱镜或衍射光栅等光谱分辨装置。在这些限制条件下，他的工作是定量的。他在室温环境中进行测量，并迅速捕捉到他的身体处于接近热平衡的状态，在这种状态下，他们通过用沸水加热到平衡状态。他的测量证实，选择性发射和吸收的物质遵守热平衡时发射和吸收的选择性相等的原理。

斯图尔特提供了一个理论证明，即对于每种选定的热辐射质量，情况都应该是分别的，但他的数学并不严格有效。据历史学家 DM 西格尔 (D.M. Siegel) 称：“他不是 19 世纪数学物理学更复杂技术的实践者；他甚至没有使用函数符号来处理光谱分布。” ^[48]他在这篇论文中没有提到热力学，尽管他确实提到了生命守恒定律。他提出，他的测量意味着辐射在传播的介质的整个深度中都被物质粒子吸收和发射。他应用亥姆霍兹互易原理来解释材料界面过程，而不是内部材料中的过程。他得出结论，他的实验表明，在热平衡的封闭空间内部，无论表面是什么物质，反射和发射的辐射热加在一起离开表面的任何部分，都与离开由烟黑组成的同一部分表面时是一样的。他没有提到理想情况下完美反射墙壁的可能性；特别是他指出高度抛光的真实物理金属吸收率非常低。

1859 年，古斯塔夫·罗伯特·基尔霍夫 (Gustav Robert Kirchhoff)不知道斯图尔特的工作，他报告了可见光的光谱吸收线和发射线波长的重合。对于热物理学来说重要的是，他还观察到，根据发射体和吸收体之间的温差，会出现亮线或暗线。^[49]

基尔霍夫继续考虑在温度为T 的不透明外壳或空腔中，发射和吸收热辐射的物体处于平衡状态。

这里使用的符号与基尔霍夫的符号不同。在这里，发射功率E ( T , i )表示一个有量纲的量，即温度为T时标有指数i的物体发射的总辐射。该物体的总吸收率a ( T , i )是无量纲的，即温度为T时腔内吸收的辐射与入射辐射的比率。（与 Balfour Stewart 的定义不同，基尔霍夫的吸收率定义并没有特别提到黑烟表面是入射辐射的来源。）因此，比率⁠E（T，i）/一（T，我）发射功率与吸收比的比值是一个有量纲的量，其量纲为发射功率，因为​​ a ( T , i )是无量纲的。同样，这里物体在温度T下的波长特定发射功率用E ( λ , T , i )表示，波长特定吸收比用a ( λ , T , i )表示。同样，比率⁠E（λ，T，i）/一个（λ，T，我）⁠发射功率与吸收率之比是一个有量纲的量，其量纲为发射功率。

在 1859 年发表的第二份报告中，基尔霍夫宣布了一项新的普遍原理或定律，并提供了理论和数学证明，尽管他没有提供辐射功率的定量测量。^[50]一些作家认为他的理论证明是无效的，现在仍然如此。^{[48] [51]}然而，他的原理经久不衰：对于相同波长的热射线，在给定温度下达到平衡状态，特定波长的发射功率与吸收率之比对于所有在该波长下发射和吸收的物体来说，都有同一个共同值。用符号表示，该定律表示波长特定的比率⁠E（λ，T，i）/一个（λ，T，我）⁠对于所有物体，即对于指数i的所有值，都有相同的值。本报告中没有提到黑体。

1860 年，基尔霍夫还不知道斯图尔特对选定辐射质量的测量，他指出，实验早已证实，对于平衡状态下的物体发射和吸收的未选定质量的总热辐射，有量纲的总辐射比⁠E（T，i）/一（T，我）⁠，对所有物体来说，都有一个共同的值，也就是说，对于物质指数i的每个值，都有一个共同的值。 ^[52]同样，在没有测量辐射功率或其他新实验数据的情况下，基尔霍夫随后为他的新原理提供了新的理论证明，即波长特定比值的普遍性⁠E（λ，T，i）/一个（λ，T，我）⁠在热平衡状态下。他的新理论证明过去和现在都被一些作者认为是无效的。 ^{[48] [51]}

但更重要的是，它依赖于“完美黑体”这一新的理论假设，这就是人们谈论基尔霍夫定律的原因。这种黑体在其无限薄的最表面表现出完全吸收。它们对应于巴尔弗·斯图尔特的参考体，具有内部辐射，涂有烟黑。它们不是普朗克后来考虑的更现实的完美黑体。普朗克的黑体仅由其内部的材料辐射和吸收；它们与相邻介质的界面只是数学表面，既不能吸收也不能发射，只能反射和透射并折射。^[53]

基尔霍夫的证明考虑了一个任意的非理想物体，标记为i ，以及各种标记为BB 的完美黑体。它要求物体在温度为T 的空腔中保持热平衡。他的证明旨在表明比率⁠E（λ，T，i）/一个（λ，T，我）⁠与非理想物体的 性质i无关

他的证明首先指出，对于波长λ和温度T，在热平衡下，所有大小和形状相同的完全黑体都具有一个相同的发射功率值E ( λ , T , BB)，其功率量纲为 。他的证明指出，完全黑体的无量纲波长特定吸收率a ( λ , T , BB)按照定义恰好为 1。那么对于完全黑体，波长特定的发射功率与吸收率之比⁠E（λ，T，BB）/a（λ，T，BB）⁠又只是E ( λ , T , BB)，其量纲为功率。基尔霍夫依次考虑了任意非理想物体的热平衡，以及相同大小和形状的完全黑体，它们位于温度为T 的平衡腔中。他认为，热辐射流在每种情况下都必须相同。因此，他认为，在热平衡时，比率⁠E（λ，T，i）/一个（λ，T，我）⁠等于E ( λ , T , BB)，现在可以表示为B _λ ( λ , T ) ，这是一个连续函数，在固定温度T时仅取决于λ，在固定波长λ时是T的增函数，在低温下对可见光为零，但在较长波长下不为零，在较高温度下对可见光波长为正值，这与任意非理想体的性质i无关。（基尔霍夫详细考虑过的几何因素在上文中已被忽略。）

因此，基尔霍夫热辐射定律可以表述为：对于任何材料，在给定温度T下，在热力学平衡下辐射和吸收，对于每个波长λ，发射功率与吸收率的比率都有一个通用值，这是完美黑体的特征，这个发射功率我们在这里用B _λ ( λ , T )表示。（对于我们的符号B _λ ( λ , T )，基尔霍夫最初的符号只是e。）^{[7] [52 ] [54 ] [55] [56] [57]}

基尔霍夫宣布，确定函数B _λ ( λ , T )是一个极其重要的问题，尽管他承认其中存在需要克服的实验困难。他认为，像其他不依赖于个体物体性质的函数一样，它将是一个简单的函数。函数B _λ ( λ , T )有时被称为“基尔霍夫（发射，通用）函数”，^{[58] [59] [60] [61]}尽管它的精确数学形式直到 40 年后才为人所知，直到 1900 年被普朗克发现。在同一时期以及之后，许多物理学家对基尔霍夫普遍性原理的理论证明进行了研究和争论。^[51]基尔霍夫后来在 1860 年表示，他的理论证明比 Balfour Stewart 的更好，在某些方面确实如此。^[48]基尔霍夫 1860 年的论文中没有提到热力学第二定律，当然也没有提到当时尚未建立的熵概念。在 1862 年的一本书中，基尔霍夫在更深入的论述中提到了他的定律与“卡诺原理”的联系，卡诺原理是第二定律的一种形式。^[62]

根据海尔格·克拉格的说法，“量子理论起源于对热辐射的研究，特别是罗伯特·基尔霍夫在 1859 年至 1860 年间首次定义的‘黑体’辐射。” ^[63]

1860 年，基尔霍夫预测，通过经验确定黑体光谱仅与温度和波长相关函数将面临困难。事实也确实如此。人们花了四十年时间改进电磁辐射测量方法，才得到可靠的结果。^[64]

1865 年，约翰·廷德尔 (John Tyndall)描述了电加热丝和碳弧发出的辐射，它们既有可见的，也有不可见的。^[65]廷德尔利用岩盐棱镜对辐射进行光谱分解，岩盐棱镜既能传递热量，也能传递可见射线，然后通过热电堆测量辐射强度。^{[66] [67]}

1880 年，安德烈-普罗斯佩-保罗·克罗瓦 (André-Prosper-Paul Crova) 发表了一张三维热辐射强度与波长和温度的关系图。^[68]他用棱镜确定了光谱变量。他通过所谓的“等温”曲线分析了表面，即单一温度的截面，横坐标为光谱变量，纵坐标为功率变量。他通过实验数据点画出平滑的曲线。它们在温度特有的光谱值处有一个峰值，并在其两侧朝向横轴下降。^{[69] [70]}即使在今天，这种光谱截面仍被广泛展示。

在 1881 年至 1886 年的一系列论文中，兰利报告了使用衍射光栅和棱镜以及他所能制造的最灵敏的探测器对热辐射光谱的测量。他报告称，峰值强度随温度升高而增加，光谱形状不以峰值为中心对称，当波长短于每个温度下的近似截止值时，强度会急剧下降，近似截止波长随温度升高而减小，峰值强度的波长随温度升高而减小，因此，对于比温度近似截止值长的短波长，强度会随温度升高而急剧增加。^[71]

1888 年，俄国物理学家 VA 迈克尔逊在阅读了兰利的著作后，发表了一篇论文，他认为未知的基尔霍夫辐射函数可以用物理来解释，用“原子振动的完全不规则性”来数学表述。^{[72] [73]}当时，普朗克还没有深入研究辐射，也不相信原子或统计物理学。^[74]迈克尔逊提出了一个温度光谱公式： 其中I _λ表示波长λ和温度θ处的特定辐射强度，B ₁和c是经验常数。 $${\displaystyle I_{\lambda }=B_{1}\theta ^{\frac {3}{2}}\exp \left(-{\frac {c}{\lambda ^{2}\theta }}\right)\lambda ^{-6},}$$

1898 年，奥托·鲁默 (Otto Lummer)和费迪南德·库尔鲍姆 (Ferdinand Kurlbaum)发表了关于他们的腔体辐射源的报道。^[75]他们的设计至今仍用于辐射测量，基本没有改变。它是一个铂盒，由隔膜隔开，内部用氧化铁涂黑。它是逐步改进的测量方法的重要组成部分，导致了普朗克定律的发现。^[76] 1901 年描述的一个版本，其内部用铬、镍和钴氧化物的混合物涂黑。^[77]

卢默和库尔鲍姆腔体辐射源的重要性在于，它是一种可通过实验获得的黑体辐射源，不同于简单暴露的白炽固体辐射，后者是合适的温度范围内最接近黑体辐射的实验近似值。以前使用的简单暴露的白炽固体发射的辐射偏离了黑体光谱，因此无法从实验中找到真正的黑体光谱。^{[78] [79]}

1897 年，普朗克首次将注意力转向黑体辐射问题。^[80] 理论和实证研究的进步使得鲁默和普林斯海姆在 1899 年写道，现有的实验证据与特定强度定律 Cλ −5e − c ⁄ λT 大致一致，其中^{C和c表示经验}可测常数， λ和T分别表示波长和温度。^{[81] [82]}出于理论原因，普朗克当时接受了这个公式，该公式对短波长有有效截止。^{[83] [84] [85]}

古斯塔夫·基尔霍夫是马克斯·普朗克的老师，他推测黑体辐射存在一条普遍定律，这被称为“基尔霍夫挑战”。^[86]理论家普朗克认为威廉·维恩发现了这条定律，普朗克在 1899 年德国物理学会会议上介绍了维恩的工作。实验物理学家奥托·鲁默、费迪南德·库尔鲍姆、恩斯特·普林斯海姆和海因里希·鲁本斯做了一些实验，似乎支持维恩定律，特别是在较高频率的短波长下，普朗克在德国物理学会上完全认可了这一点，以至于它开始被称为维恩-普朗克定律。^[87]然而，到 1900 年 9 月，实验人员已经毫无疑问地证明了维恩-普朗克定律在较长的波长下不成立。他们于 10 月 19 日提交了他们的数据。普朗克从他的朋友鲁本斯那里得知了这一消息，并在几天内迅速创建了一个公式。^[88]同年 6 月，瑞利勋爵基于广为接受的均分理论创建了一个适用于短低频波长的公式。^[89]因此，普朗克提交了一个结合瑞利定律（或类似的均分理论）和维恩定律的公式，该公式将根据波长对其中一个定律或另一个定律进行加权，以匹配实验数据。然而，尽管这个方程成立，但普朗克本人表示，除非他能将这个从“幸运直觉”中得出的公式解释为物理学中“真正意义”的公式，否则它就没有真正的意义。^[90]普朗克解释说，此后就是他一生中最艰难的工作。普朗克不相信原子，也不认为热力学第二定律应该是统计的，因为概率不能提供绝对的答案，而玻尔兹曼的熵定律建立在原子假设之上，是统计的。但普朗克无法找到一种方法来调和他的黑体方程与麦克斯韦波动方程等连续定律。因此，普朗克称自己“绝望之举” ^[91] ，他求助于玻尔兹曼原子熵定律，因为这是使他的方程成立的唯一定律。因此，他使用玻尔兹曼常数k和他的新常数h来解释黑体辐射定律，该定律通过他发表的论文广为人知。^{[92] [93]}

马克斯·普朗克于 1900 年 10 月 19 日提出了斯图尔特-基尔霍夫定律^{[94] [95] ，是对}威廉·维恩于 1896 年发表的维恩近似的改进，该近似在短波长（高频）下符合实验数据，但在长波长（低频）下偏离实验数据。^[41] 1900 年 6 月，基于启发式理论考虑，瑞利提出了一个公式^[96]，他建议可以通过实验来检验。 该建议是斯图尔特-基尔霍夫通用函数可能采用c ₁ Tλ ⁻⁴ exp(– ⁠c2_​/λ⁠ )。这并不是著名的瑞利-金斯公式8πkBTλ − 4 ^，该公式直到 1905 年才出现， ^[38]不过对于长波长，它的确简化为后者，而长波长正是本文所讨论的。根据克莱因的说法， _[ ^80]人们可能推测，普朗克可能已经看到了这个建议，尽管他在 1900 年和 1901 年的论文中没有提到它。普朗克一定知道其他各种提出的公式。 ^{[64] [97]} 1900 年 10 月 7 日，鲁本斯告诉普朗克，在互补域（长波长、低频），而且只有在那里，瑞利 1900 年的公式才能很好地拟合观测数据。 ^[97]

对于长波长，瑞利 1900 年的启发式公式近似地意味着能量与温度成正比，U _λ = const. T。^{[80] [97] [98]}众所周知⁠差分/λ_​⁠ = ⁠1/电视⁠这导致了⁠差分/λ_​⁠ = ⁠常量。/λ_​⁠并从那里到⁠硫^​​/_λ 2^​⁠ = − ⁠常量。/λ ²_​⁠对于长波长。但对于短波长，维恩公式可得出⁠1/电视⁠ = − const. ln U _λ + const.由此至⁠硫^​​/_λ 2^​⁠ = − ⁠常量。/λ_​⁠短波长。普朗克可能将这两个启发式公式（长波长和短波长）拼凑在一起， ^{[97] [99]}得出一个公式^[94] $${\displaystyle {\frac {d^{2}S}{dU_{\lambda }^{2}}}={\frac {\alpha }{U_{\lambda }(\beta +U_{\lambda })}}.}$$

这使得普朗克得出了这个公式 ，其中普朗克使用符号C和c来表示经验拟合常数。 $${\displaystyle B_{\lambda }(T)={\frac {C\lambda ^{-5}}{e^{\frac {c}{\lambda T}}-1}},}$$

普朗克将这个结果寄给了鲁本斯，鲁本斯将其与他和库尔鲍姆的观测数据进行了比较，发现它对所有波长的拟合度都非常好。1900 年 10 月 19 日，鲁本斯和库尔鲍姆简要报告了数据的拟合情况，^[100]普朗克也做了一个简短的介绍，从理论上解释了他的公式。^[94]一周之内，鲁本斯和库尔鲍姆更详细地报告了他们的测量结果，证实了普朗克定律。他们用于较长波长辐射光谱分辨的技术称为残余射线法。射线在抛光的晶体表面反复反射，穿过整个过程的射线是“残余的”，是会被特定材料制成的晶体优先反射的波长。^{[101] [102] [103]}

普朗克发现了符合经验的函数后，便构建了该定律的物理推导。他的思考围绕着熵，而不是直接围绕温度。普朗克考虑了一个具有完美反射壁的腔体；腔内有有限多个不同但结构相同的谐振振荡体，这些振荡体具有确定的幅度，每个振荡体都有几个这样的振荡器，每个振荡器具有有限多个特征频率。对于普朗克来说，这些假设的振荡器纯粹是虚构的理论研究探测器，他说，这样的振荡器不需要“真的存在于自然界的某个地方，只要它们的存在和特性符合热力学和电动力学定律”。^[104]普朗克没有为他的谐振振荡器假设赋予任何明确的物理意义，而是将其作为一种数学手段提出，使他能够推导出与所有波长的经验数据相匹配的黑体光谱的单一表达式。^{[105]他试探性地提到了这种振荡器与}原子的可能联系。从某种意义上说，振荡器对应于普朗克的碳斑点；无论腔体尺寸如何，碳斑点的尺寸都可以很小，只要碳斑点能够有效地在辐射波长模式之间转换能量。^[97]

普朗克部分遵循了玻尔兹曼为气体分子开创的启发式计算方法，他考虑了在他假设的带电物质振荡器的不同模式中分配电磁能量的可能方式。普朗克接受了玻尔兹曼提出的概率方法，这与他之前的立场完全不同，在此之前，他一直有意反对玻尔兹曼提出的这种想法。^[106]用普朗克的话来说，“我认为 [量子假设] 是一个纯粹的形式假设，除了这一点之外，我没有做太多思考：我在任何情况下、不惜一切代价都得到了积极的结果。” ^[107]玻尔兹曼启发式地将能量分布在任意的数学量子 ϵ中，他继续使它的量级趋于零，因为有限量ϵ只是为了在数学计算概率时进行明确的计数，没有物理意义。参照一个新的自然普适常数h，^[108]普朗克假设，在有限多个特征频率的多个振子中，总能量以一定物理能量单位ϵ的整数倍分配给每个振子，该能量单位是各个特征频率所特有的。^{[95] [109] [110] [111]}他提出的新的自然普适常数h，现在被称为普朗克常数。

普朗克进一步解释说^[95]，能量的相应确定单位ϵ应该与假设振荡器的相应特征振荡频率ν成正比，并于 1901 年用比例常数h表示这一点：^{[112] [113]} $${\displaystyle \epsilon =h\nu .}$$

普朗克并没有提出在自由空间中传播的光是量子化的。^{[114] [115] [116]}自由电磁场的量子化思想后来得到发展，并最终融入我们现在所知的量子场论。^[117]

1906 年，普朗克承认他想象中的谐振器具有线性动力学，无法为频率之间的能量转换提供物理解释。^{[118] [119]}当今物理学遵循爱因斯坦的观点，用原子的量子激发性来解释频率之间的转换。普朗克认为，在一个具有完美反射壁且不存在任何物质的腔体中，电磁场无法在频率分量之间交换能量。^[120]这是因为麦克斯韦方程组的线性。^[121]当今的量子场论预测，在没有物质的情况下，电磁场遵循非线性方程，从这个意义上说确实会发生自相互作用。^{[122] [123]}这种在没有物质的情况下的相互作用尚未直接测量，因为它需要非常高的强度和非常灵敏、低噪声的探测器，而这些探测器仍在建造过程中。^{[122] [124]}普朗克认为，没有相互作用的场既不遵循也不违反经典的能量均分原理，^{[125] [126]}而是保持与引入时完全相同的状态，而不是演变成黑体场。^[127]因此，他的力学假设的线性使得普朗克无法对热力学平衡热辐射场的熵最大化做出力学解释。 这就是为什么他不得不诉诸玻尔兹曼的概率论证。^{[128] [129]}

普朗克定律可视为实现了古斯塔夫·基尔霍夫的预言，即他的热辐射定律具有最高重要性。普朗克在对自己定律的成熟阐述中，为基尔霍夫定律提供了全面而详细的理论证明。^[130]在此之前，该定律的理论证明有时存在争议，部分原因是据说它依赖于非物理的理论对象，例如基尔霍夫的完美吸收无限薄的黑色表面。^[131]

直到普朗克对能量或作用的抽象元素做出启发式假设五年后，阿尔伯特·爱因斯坦才在 1905 年构想出真正存在的光量子^[132]，为黑体辐射、光致发光、光电效应和紫外光对气体的电离提供了革命性的解释。1905 年，“爱因斯坦认为普朗克的理论不能与光量子的概念相一致，他在 1906 年纠正了这个错误。” ^[133]与普朗克当时的信念相反，爱因斯坦提出了一个模型和公式，即光以空间点中的能量量子的形式在自由空间中发射、吸收和传播。^[132]作为对其推理的介绍，爱因斯坦重述了普朗克假设的谐振材料电振荡器作为辐射源和辐射汇的模型，但随后他提出了一个与该模型无关的新论点，但部分基于维恩的热力学论证，其中普朗克公式ϵ = hν不起作用。^[134]爱因斯坦给出了这种量子的能量含量，形式为⁠受体βν/否⁠。因此，爱因斯坦的观点与普朗克所持的光的波动理论相矛盾。1910 年，爱因斯坦在批评普朗克寄给他的一份手稿时，知道普朗克是爱因斯坦狭义相对论的坚定支持者，爱因斯坦写信给普朗克说：“在我看来，如果不假设以太，能量在空间中连续分布似乎是荒谬的。” ^[135]

根据托马斯·库恩的说法，直到 1908 年，普朗克才或多或少接受了爱因斯坦关于热辐射物理学中物理离散性与抽象数学离散性不同的部分论据。同样在 1908 年，考虑到爱因斯坦关于量子传播的提议，普朗克认为这种革命性的举措也许是不必要的。^[136]在此之前，普朗克一直认为，作用量子的离散性既不存在于他的共振振荡器中，也不存在于热辐射传播中。库恩写道，在普朗克的早期论文和 1906 年的专著中，^[137] “没有提到不连续性，也没有谈论对振荡器能量的限制，也没有提到任何像U = nhν这样的公式。”库恩指出，他对普朗克 1900 年和 1901 年论文以及 1906 年专著的研究^[137]使他得出了“异端”结论，这与其他人的普遍假设相反，他们只从后来的、不合时宜的观点来看待普朗克的作品^[138] 。库恩的结论发现，直到 1908 年，普朗克一直坚持他的“第一理论”，这一结论已被其他历史学家接受^{[139] 。}

1912 年，普朗克在其专著第二版中坚持反对爱因斯坦的光量子理论。他详细提出，虚拟材料谐振器对光的吸收可能是连续的，在平衡状态下以恒定速率发生，与量子吸收不同。只有发射是量子的。^{[121] [140]}这有时被称为普朗克的“第二理论”。^[141]

直到1919年，普朗克在他的专著第三版中才或多或少地接受了他的“第三种理论”，即光的发射和吸收都是量子的。^[142]

1911 年，保罗·艾伦费斯特 (Paul Ehrenfest)给出了一个生动的术语“紫外灾变”，来描述当经典统计力学的均分定理(错误地) 应用于黑体辐射时，腔内总能量趋于无穷大这一矛盾结果。 ^{[143] [144]}但这并不是普朗克的想法，因为他并没有尝试应用均分理论：当他在 1900 年发现它时，他并没有注意到任何类型的“灾变”。^{[83] [84] [85] [80] [145]}瑞利勋爵 (Lord Rayleigh)于 1900 年首次注意到它，^{[96] [146] [147]}然后詹姆斯·金斯爵士 (Sir James Jeans ) 于 1901 年^[148]注意到它； 1905年，爱因斯坦为了支持光以离散包（后来被称为“光子”）传播的观点，也提出了这一观点；随后瑞利^[39]和金斯也提出了这一观点。^{[38] [149] [150] [151]}

1913年，玻尔给出了另一个公式，该公式对hν 的物理含义有进一步的不同。^{[34] [35] [36] [152] [153] [154]}与普朗克和爱因斯坦的公式相比，玻尔公式明确而绝对地提到了原子的能级。玻尔公式为W _{τ 2} − W _{τ 1} = hν ，其中W _{τ 2}和W _{τ 1}表示原子量子态的能级，量子数为τ ₂和τ ₁。符号ν表示原子在两个量子态之间穿过时可以发射或吸收的辐射量子的频率。与普朗克模型相比，频率与描述这些量子态本身的频率没有直接关系。 ${\displaystyle \nu }$

后来，在 1924 年，萨蒂延德拉·纳特·玻色发展了光子统计力学理论，从而可以理论推导普朗克定律。^[155] “光子”这个词实际上是由 G·N·刘易斯在 1926 年发明的，^[156]他错误地认为光子是守恒的，这与玻色-爱因斯坦统计相反；尽管如此，“光子”这个词还是被用来表达爱因斯坦关于光传播的分组性质的假设。在一个被真空隔离的电磁场中，在一个具有完美反射壁的容器中，就像普朗克所考虑的那样，根据爱因斯坦 1905 年的模型，光子确实是会守恒的，但刘易斯指的是一个光子场，它被认为是一个相对于有重量物质封闭的系统，但可以与周围的有重量物质系统交换电磁能，他错误地想象光子仍然是守恒的，存储在原子内部。

最终，普朗克黑体辐射定律促成了爱因斯坦提出携带线性动量的光量子概念^{[34] [132] ，这成为}量子力学发展的基本基础。

普朗克力学假设的上述线性不允许频率分量之间的能量相互作用，这一假设在 1925 年被海森堡的原始量子力学所取代。海森堡在 1925 年 7 月 29 日提交的论文中，他的理论解释了玻尔 1913 年提出的上述公式。它承认非线性振荡器是原子量子态的模型，在发射或吸收辐射量子时，允许它们自身内部多个离散傅立叶频率分量之间发生能量相互作用。辐射量子的频率是原子内部亚稳态振荡量子态之间确定耦合的频率。^{[157] [158]}当时，海森堡对矩阵代数一无所知，但马克斯·玻恩阅读了海森堡论文的手稿，认识到海森堡理论的矩阵特性。随后，玻恩和约尔当发表了明确的量子力学矩阵理论，该理论基于海森堡最初的量子力学，但形式上与之截然不同；玻恩和约尔当矩阵理论就是今天所谓的矩阵力学。^{[159] [160] [161]}海森堡对普朗克振子的解释是，它是一种非线性效应，表现为辐射发射或吸收瞬态过程的傅里叶模式，这说明了为什么普朗克振子虽然被视为经典物理学可能设想的持久物理对象，但不能充分解释这种现象。

如今，作为光量子能量的表述，我们经常发现公式E = ħω，其中ħ = ⁠时长/2π⁠， ω = 2π ν表示角频率， ^{[162] [163 ] [164] [165] [166]}较少见的是等效公式E = hν。 ^{[165] [166] [167] [168] [169]}这个关于真实存在和传播的光量子的表述，基于爱因斯坦的理论，其物理含义与普朗克上述关于抽象能量单位在他假设的共振材料振荡器之间分配的 表述ϵ = hν不同。

海尔格·克拉格在《物理世界》上发表的一篇文章记述了这段历史。^[111]

• 发射率
• 辐射
• 佐久间–服部方程

• 辐射概述
• 黑体辐射——互动模拟普朗克定律
• 科学世界关于普朗克定律的条目