量子力学

这是关于
量子力学
${\displaystyle i\hbar {\frac {d}{dt}}|\Psi \rangle ={\hat {H}}|\Psi \rangle }$ 薛定谔方程
介绍 词汇表 历史
背景 经典力学 旧量子理论 Bra–ket 符号 哈密​​顿量 干涉
基本面 互补性 退相干 纠缠 能级 测量 非局域性 量子数 状态 叠加 对称 隧道施工 不确定 波函数 坍塌
实验 贝尔不等式 CHSH 不等式 戴维森–格默 双缝 埃利祖尔–瓦依德曼 弗兰克-赫兹 莱格特不等式 Leggett–Garg 不等式 马赫-曾德 波普尔 量子擦除器 延迟选择 薛定谔的猫 斯特恩-格拉赫 惠勒的延迟选择
配方 概述 海森堡 相互作用 矩阵 相空间 薛定谔 历史总和（路径积分）
方程式 狄拉克 克莱因-戈登 泡利 里德伯 薛定谔
解释 贝叶斯 一致的历史 哥本哈根 德布罗意-玻姆 合奏 隐变量 当地的 超决定论 多重世界 目标崩溃 量子逻辑 关系型 交易性 冯·诺依曼-维格纳
高级主题 相对论量子力学 量子场论 量子信息科学 量子计算 量子混沌 EPR悖论 密度矩阵 散射理论 量子统计力学 量子机器学习
科学家 阿哈罗诺夫 钟 贝特 布莱克特 布洛赫 波姆 波尔 出生 博斯 德布罗意 康普顿 狄拉克 戴维森 德拜 埃伦菲斯特 爱因斯坦 埃弗雷特 福克 费米 费曼 格劳伯 古兹维勒 海森堡 希尔伯特 约旦 克莱默斯 羊肉 兰道 劳厄 Moseley Millikan Onnes Pauli Planck Rabi Raman Rydberg Schrödinger Simmons Sommerfeld von Neumann Weyl Wien Wigner Zeeman Zeilinger
v t e

量子力学是描述原子尺度及以下自然界行为的基本理论。^{[2] ：1.1}它是所有量子物理学的基础，包括量子化学、量子场论、量子技术和量子信息科学。

量子力学可以描述许多经典物理学无法描述的系统。经典物理学可以在普通（宏观和（光学）微观）尺度上描述自然界的许多方面，但不足以在非常小的亚微观（原子和亚原子）尺度上描述它们。经典物理学中的大多数理论都可以从量子力学的近似值中推导出来，在宏观/微观尺度上有效。^[3]

量子系统具有被量化为能量、动量、角动量和其他量的离散值的束缚态，而经典系统则不同，经典系统可以连续测量这些量。量子系统的测量表现出粒子和波的特性（波粒二象性），并且在给定一组完整的初始条件（不确定性原理）的情况下，在测量之前预测物理量值的准确度是有限的。

量子力学逐渐从解释与经典物理学无法调和的观察结果的理论中产生，例如马克斯·普朗克 1900 年对黑体辐射问题的解，以及阿尔伯特·爱因斯坦1905年论文中关于能量和频率之间的对应关系的解释，该论文解释了光电效应。这些早期理解微观现象的尝试现在被称为“旧量子理论”，导致了尼尔斯·玻尔、埃尔温·薛定谔、维尔纳·海森堡、马克斯·玻恩、保罗·狄拉克等人在 20 世纪 20 年代中期对量子力学进行了全面发展。现代理论以各种专门发展的数学形式来表述。其中一种形式中，一个称为波函数的数学实体以概率幅的形式提供了关于粒子能量、动量和其他物理性质的测量结果的信息。

量子力学可以计算物理系统的性质和行为。它通常应用于微观系统：分子、原子和亚原子粒子。事实证明，它适用于具有数千个原子的复杂分子，^[4]但将其应用于人类会引发哲学问题，例如维格纳的朋友，而将其应用于整个宇宙仍是推测性的。^[5]量子力学的预测已通过实验得到极高的准确度验证。例如，用于光和物质相互作用的量子力学的改进，称为量子电动力学(QED)，在预测电子的磁性时，已被证明与实验结果的一致性在 10 ¹²分之 1 以内。 ^[6]

该理论的一个基本特征是它通常不能准确地预测会发生什么，而只能给出概率。从数学上讲，概率是通过取复数绝对值的平方来得出的，该复数称为概率幅。这被称为玻恩规则，以物理学家马克斯·玻恩的名字命名。例如，像电子这样的量子粒子可以用波函数来描述，该波函数将空间中的每个点与概率幅相关联。将玻恩规则应用于这些振幅，可以得到在进行测量实验时电子所在位置的概率密度函数。这是该理论所能做到的最好的事情了；它不能肯定地说出电子会在哪里找到。薛定谔方程将某一时刻的概率幅集合与另一时刻的概率幅集合联系起来。^{[7] ：67–87}

量子力学数学规则的一个结果是可测量量之间的可预测性权衡。这种不确定性原理最著名的形式是，无论量子粒子是如何制备的，或者对它的实验安排得多么仔细，都不可能同时精确预测其位置的测量值和动量的测量值。 [ ^{7] ：427–435}

量子力学数学规则的另一个结果是量子干涉现象，通常用双缝实验来说明。在这个实验的基本版本中，一个相干光源，比如一束激光，照射到一个被两个平行狭缝刺穿的平板上，穿过狭缝的光可以在平板后面的屏幕上观察到。^{[8] ： 102–111  [2] ： 1.1–1.8}光的波动性质导致穿过两个狭缝的光波发生干涉，在屏幕上产生明暗带——如果光由经典粒子组成，这是不可能发生的结果。^[8]然而，人们总是发现光在屏幕上以离散点的形式被吸收，作为单独的粒子而不是波；干涉图案是通过这些粒子撞击屏幕的不同密度出现的。此外，在狭缝处安装探测器的实验版本发现，每个探测到的光子都会穿过一条狭缝（就像经典粒子一样），而不是同时穿过两条狭缝（就像波一样）。^{[8] : 109  [9] [10]}然而，此类实验表明，如果探测到粒子穿过哪条狭缝，它们就不会形成干涉图案。这种行为被称为波粒二象性。除光之外，电子、原子和分子在射向双缝时都表现出相同的二象行为。^[2]

量子力学预测的另一个非经典现象是量子隧穿：一个粒子冲向势垒，即使它的动能小于势垒的最大值，它也能穿过势垒。^[11]在经典力学中，这个粒子会被困住。量子隧穿有几个重要的后果，使放射性衰变、恒星中的核聚变以及扫描隧道显微镜、隧道二极管和隧道场效应晶体管等应用成为可能。^{[12] [13]}

当量子系统相互作用时，其结果可能是产生量子纠缠：它们的属性变得如此紧密地交织在一起，以至于不再可能仅根据各个部分来描述整体。埃尔温·薛定谔称纠缠为“……量子力学的特征，它强制其完全背离经典思维”。^[14]量子纠缠使量子计算成为可能，并且是量子通信协议的一部分，例如量子密钥分发和超密集编码。^[15]与普遍的误解相反，纠缠不允许发送比光更快的信号，正如无通信定理所证明的那样。^[15]

纠缠带来的另一种可能性是测试“隐变量”，即比量子理论本身所涉及的量更基本的假设性质，了解这些性质可以做出比量子理论更精确的预测。一系列结果，其中最重要的就是贝尔定理，已经证明，这类隐变量理论的大类实际上与量子物理不相容。根据贝尔定理，如果自然界实际上按照任何局部隐变量理论运行，那么贝尔测试的结果将受到某种特定的、可量化的限制。许多贝尔测试已经进行，结果显示与局部隐变量施加的约束不相容。^{[16] [17]}

如果不介绍所涉及的数学，就不可能以肤浅的方式呈现这些概念；理解量子力学不仅需要操纵复数，还需要线性代数、微分方程、群论和其他更高级的学科。^{[18] [19]}因此，本文将提出量子力学的数学公式，并调查其在一些有用且经常研究的例子中的应用。

在量子力学的数学严格表述中，量子力学系统的状态是属于（可分离的）复希尔伯特空间的矢量。假设这个矢量在希尔伯特空间内积下是归一化的，即它服从，并且在模1（全局相）的复数下是定义明确的，即和表示相同的物理系统。换句话说，可能的状态是希尔伯特空间的射影空间中的点，通常称为复射影空间。这个希尔伯特空间的确切性质取决于系统——例如，用于描述位置和动量的希尔伯特空间是复平方可积函数的空间，而用于单个质子自旋的希尔伯特空间只是具有通常内积的二维复矢量空间。 ${\displaystyle \psi }$ ${\displaystyle {\mathcal {H}}}$${\displaystyle \langle \psi ,\psi \rangle =1}$${\displaystyle \psi }$${\displaystyle e^{i\alpha }\psi }$${\displaystyle L^{2}(\mathbb {C} )}$${\displaystyle \mathbb {C} ^{2}}$

位置、动量、能量、自旋等物理量都由可观测量表示，可观测量是作用于希尔伯特空间的厄米（更准确地说，自伴随）线性算子。量子态可以是可观测量的特征向量，在这种情况下它被称为特征态，而相关的特征值对应于该特征态中可观测量的值。更一般地，量子态将是特征态的线性组合，称为量子叠加。当测量可观测量时，结果将是它的一个特征值，概率由波恩规则给出：在最简单的情况下，特征值是非退化的，概率由给出，其中是其相关的特征向量。更一般地，特征值是退化的，概率由给出，其中是到其相关特征空间的投影仪。在连续情况下，这些公式给出的是概率密度。 ${\displaystyle \lambda }$${\displaystyle |\langle {\vec {\lambda }},\psi \rangle |^{2}}$${\displaystyle {\vec {\lambda }}}$${\displaystyle \langle \psi ,P_{\lambda }\psi \rangle }$${\displaystyle P_{\lambda }}$

测量后，如果获得了结果，则假定量子态在非简并情况下坍缩为，在一般情况下坍缩为 。因此，量子力学的概率性质源于测量行为。这是量子系统最难理解的方面之一。这是著名的玻尔-爱因斯坦辩论的中心话题，在辩论中，两位科学家试图通过思想实验来阐明这些基本原理。在量子力学提出后的几十年里，人们对“测量”的构成问题进行了广泛的研究。人们提出了量子力学的新解释，这些解释摒弃了“波函数坍缩”的概念（例如，参见多重世界解释）。其基本思想是，当量子系统与测量仪器相互作用时，它们各自的波函数会纠缠在一起，因此原始量子系统不再作为独立实体存在（参见量子力学中的测量^[20]）。 ${\displaystyle \lambda }$${\displaystyle {\vec {\lambda }}}$${\textstyle P_{\lambda }\psi {\big /}\!{\sqrt {\langle \psi ,P_{\lambda }\psi \rangle }}}$

量子态的时间演化可以用薛定谔方程来描述：

${\displaystyle i\hbar {\frac {\partial }{\partial t}}\psi (t)=H\psi (t).}$

这里表示哈密顿量，即对应于系统总能量的可观测量，是约化普朗克常数。引入常数，当量子系统可以用经典系统近似时，哈密顿量就简化为经典哈密顿量；在一定极限下进行这种近似的能力称为对应原理。 ${\displaystyle H}$${\displaystyle \hbar }$${\displaystyle i\hbar }$

该微分方程的解为

${\displaystyle \psi (t)=e^{-iHt/\hbar }\psi (0).}$

这个算符被称为时间演化算符，它的关键性质是幺正性。这个时间演化是确定性的，即给定一个初始量子态，它就能明确预测以后任何时间的量子态。^[21]${\displaystyle U(t)=e^{-iHt/\hbar }}$${\displaystyle \psi (0)}$${\displaystyle \psi (t)}$

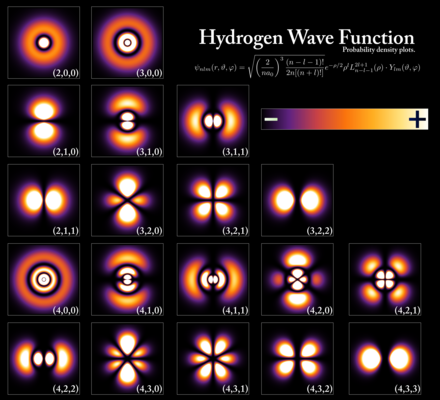
一些波函数产生与时间无关的概率分布，例如哈密顿量的本征态。^{[7] ：133–137}经典力学中动态处理的许多系统都由这种“静态”波函数描述。例如，未激发原子中的单个电子在经典上被描绘成围绕原子核沿圆形轨迹移动的粒子，而在量子力学中，它被描述为围绕原子核的静态波函数。例如，未激发氢原子的电子波函数是一个球对称函数，称为s轨道（图 1）。

薛定谔方程的解析解只存在于极少数相对简单的哈密顿模型中，包括量子谐振子、盒子中的粒子、二氢阳离子和氢原子。即使是只含有两个电子的氦原子，也无法对其进行完全解析处理，无法得到封闭形式的解。^{[22] [23] [24]}

不过，也有寻找近似解的技术。一种方法称为微扰理论，它使用简单量子力学模型的解析结果，通过（例如）添加弱势能，为相关但更复杂的模型创建结果。 [ ^{7] : 793}另一种近似方法适用于量子力学仅产生与经典行为有微小偏差的系统。然后可以根据经典运动计算这些偏差。^{[7] : 849}

基本量子形式主义的一个推论是不确定性原理。它最常见的形式是，任何量子粒子的制备都不能同时精确预测其位置的测量值和动量的测量值。^{[25] [26]位置和动量都是可观测量，这意味着它们可以用}厄米算符来表示。位置算符和动量算符不交换，而是满足正则交换关系： ${\displaystyle {\hat {X}}}$${\displaystyle {\hat {P}}}$

${\displaystyle [{\hat {X}},{\hat {P}}]=i\hbar .}$

给定一个量子态，Born 规则让我们能够计算和的期望值，以及它们的幂。用标准差定义可观测量的不确定性，我们得到 ${\displaystyle X}$${\displaystyle P}$

${\displaystyle \sigma _{X}={\textstyle {\sqrt {\left\langle X^{2}\right\rangle -\left\langle X\right\rangle ^{2}}}},}$

对于动量也一样：

${\displaystyle \sigma _{P}={\sqrt {\left\langle P^{2}\right\rangle -\left\langle P\right\rangle ^{2}}}.}$

不确定性原理指出

${\displaystyle \sigma _{X}\sigma _{P}\geq {\frac {\hbar }{2}}.}$

原则上，两个标准差都可以任意小，但不能同时小。^[27]这个不等式可以推广到任意对自伴算子和。这两个算子的 交换子是${\displaystyle A}$${\displaystyle B}$

${\displaystyle [A,B]=AB-BA,}$

这给出了标准差乘积的下限：

${\displaystyle \sigma _{A}\sigma _{B}\geq {\tfrac {1}{2}}\left|{\bigl \langle }[A,B]{\bigr \rangle }\right|.}$

正则对易关系的另一个推论是位置算符和动量算符互为傅里叶变换，因此根据物体的动量对物体的描述是根据其位置描述的傅里叶变换。动量依赖性是位置依赖性的傅里叶变换，这一事实意味着动量算符等价于（最多为一个因子）根据位置求导，因为在傅里叶分析中，微分对应于对偶空间中的乘法。这就是为什么在位置空间中的量子方程中，动量被替换为，特别是在位置空间中的非相对论薛定谔方程中，动量平方项被替换为拉普拉斯乘以。^[25]${\displaystyle i/\hbar }$${\displaystyle p_{i}}$${\displaystyle -i\hbar {\frac {\partial }{\partial x}}}$${\displaystyle -\hbar ^{2}}$

当将两个不同的量子系统放在一起考虑时，组合系统的希尔伯特空间是两个组成部分的希尔伯特空间的张量积。例如，假设A和B是两个量子系统，其希尔伯特空间分别为和。则复合系统的希尔伯特空间为 ${\displaystyle {\mathcal {H}}_{A}}$${\displaystyle {\mathcal {H}}_{B}}$

${\displaystyle {\mathcal {H}}_{AB}={\mathcal {H}}_{A}\otimes {\mathcal {H}}_{B}.}$

如果第一个系统的状态为矢量，第二个系统的状态为，则复合系统的状态为 ${\displaystyle \psi _{A}}$${\displaystyle \psi _{B}}$

${\displaystyle \psi _{A}\otimes \psi _{B}.}$

然而，并非联合希尔伯特空间中的所有状态都可以写成这种形式，因为叠加原理意味着这些“可分离”或“乘积状态”的线性组合也是有效的。例如，如果和都是系统 的可能状态，同样和都是系统 的可能状态，那么 ${\displaystyle {\mathcal {H}}_{AB}}$${\displaystyle \psi _{A}}$${\displaystyle \phi _{A}}$${\displaystyle A}$${\displaystyle \psi _{B}}$${\displaystyle \phi _{B}}$${\displaystyle B}$

${\displaystyle {\tfrac {1}{\sqrt {2}}}\left(\psi _{A}\otimes \psi _{B}+\phi _{A}\otimes \phi _{B}\right)}$

是不可分离的有效联合状态。不可分离的状态称为纠缠态。^{[28] [29]}

如果复合系统的状态是纠缠的，则不可能用状态向量描述组件系统A或系统B。我们可以改为定义简化密度矩阵来描述仅对任一组件系统进行测量即可获得的统计数据。但这必然会导致信息丢失：仅了解各个系统的简化密度矩阵不足以重建复合系统的状态。^{[28] [29]}正如密度矩阵指定较大系统的子系统的状态一样，类似地，正算子值测度(POVM) 描述了对较大系统进行测量对子系统的影响。POVM 广泛应用于量子信息论。^{[28] [30]}

如上所述，纠缠是测量过程模型的一个关键特征，测量过程中，仪器与被测系统产生纠缠。与其所在环境相互作用的系统通常会与该环境产生纠缠，这种现象称为量子退相干。这可以解释为什么在实践中，量子效应很难在比微观更大的系统中观察到。^[31]

量子力学有许多数学上等价的表述。其中最古老和最常见的是保罗·狄拉克提出的“变换理论” ，它统一并概括了量子力学的两种最早表述——矩阵力学（由维尔纳·海森堡发明）和波动力学（由埃尔温·薛定谔发明）。^[32]量子力学的另一种表述是费曼的路径积分表述，其中量子力学振幅被视为初始状态和最终状态之间所有可能的经典和非经典路径的总和。这是经典力学中作用原理的量子力学对应物。^[33]

哈密​​顿量被称为时间演化的生成器，因为它为 的每个值定义了一个幺正时间演化算子。从和之间的关系可以得出，任何与 交换的可观测量都将守恒：它的期望值不会随时间而改变。^{[7] : 471}这个陈述概括了，因为在数学上，任何厄米算子都可以生成一个由变量 参数化的幺正算子家族。在 生成的演化下，任何与 交换的可观测量都将守恒。此外，如果在 下的演化守恒，那么在 生成的演化下也守恒。这意味着艾米·诺特在经典（拉格朗日）力学中证明的结果的量子版本：对于哈密顿量的每一个可微对称性，都存在一个相应的守恒定律。 ${\displaystyle H}$${\displaystyle U(t)=e^{-iHt/\hbar }}$${\displaystyle t}$${\displaystyle U(t)}$${\displaystyle H}$${\displaystyle A}$${\displaystyle H}$${\displaystyle A}$${\displaystyle t}$${\displaystyle A}$${\displaystyle B}$${\displaystyle A}$${\displaystyle B}$${\displaystyle A}$${\displaystyle A}$${\displaystyle B}$

具有位置自由度的量子系统最简单的例子是单个空间维度中的自由粒子。自由粒子不受外界影响，因此其哈密顿量仅由其动能组成：

${\displaystyle H={\frac {1}{2m}}P^{2}=-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}}{dx^{2}}}.}$

薛定谔方程的通解为

${\displaystyle \psi (x,t)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }{\hat {\psi }}(k,0)e^{i(kx-{\frac {\hbar k^{2}}{2m}}t)}\mathrm {d} k,}$

它是所有可能平面波 的叠加，是具有动量的动量算符的本征态。叠加的系数是，它是初始量子态的傅里叶变换。 ${\displaystyle e^{i(kx-{\frac {\hbar k^{2}}{2m}}t)}}$${\displaystyle p=\hbar k}$${\displaystyle {\hat {\psi }}(k,0)}$${\displaystyle \psi (x,0)}$

解不可能是单个动量本征态，或者单个位置本征态，因为它们不是可归一化的量子态。^{[注 1]}相反，我们可以考虑一个高斯波包：

${\displaystyle \psi (x,0)={\frac {1}{\sqrt[{4}]{\pi a}}}e^{-{\frac {x^{2}}{2a}}}}$

具有傅里叶变换，因此具有动量分布

${\displaystyle {\hat {\psi }}(k,0)={\sqrt[{4}]{\frac {a}{\pi }}}e^{-{\frac {ak^{2}}{2}}}.}$

我们看到，当我们使 变小的时候，位置的差异会变小，但动量的差异会变大。相反，通过使 变大，我们使动量的差异变小，但位置的差异会变大。这说明了不确定性原理。 ${\displaystyle a}$${\displaystyle a}$

当我们让高斯波包随时间演化时，我们看到它的中心以恒定速度在空间中移动（就像没有作用力的经典粒子一样）。然而，随着时间的推移，波包也会扩散，这意味着位置变得越来越不确定。然而，动量的不确定性保持不变。^[34]

一维势能盒中的粒子是数学上最简单的例子，其中约束导致能级量化。盒子被定义为在某个区域内处处具有零势能，因此在该区域外处处具有无限势能。[ ^{25] : 77–78}对于方向上的一维情况，时间无关的薛定谔方程可以写成 ${\displaystyle x}$

${\displaystyle -{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}\psi }{dx^{2}}}=E\psi .}$

微分算子定义为

${\displaystyle {\hat {p}}_{x}=-i\hbar {\frac {d}{dx}}}$上面的方程让人想起经典的动能模拟，

${\displaystyle {\frac {1}{2m}}{\hat {p}}_{x}^{2}=E,}$

在这种情况下，状态的能量与粒子的动能一致。 ${\displaystyle \psi }$${\displaystyle E}$

盒子中粒子的薛定谔方程的通解为

${\displaystyle \psi (x)=Ae^{ikx}+Be^{-ikx}\qquad \qquad E={\frac {\hbar ^{2}k^{2}}{2m}}}$

或者，根据欧拉公式，

${\displaystyle \psi (x)=C\sin(kx)+D\cos(kx).\!}$

盒子的无限势壁决定了和在和的值，其中必须为零。因此，在， ${\displaystyle C,D,}$${\displaystyle k}$${\displaystyle x=0}$${\displaystyle x=L}$${\displaystyle \psi }$${\displaystyle x=0}$

${\displaystyle \psi (0)=0=C\sin(0)+D\cos(0)=D}$

和。在， ${\displaystyle D=0}$${\displaystyle x=L}$

${\displaystyle \psi (L)=0=C\sin(kL),}$

其中不能为零，因为这会与具有范数 1 的公设相冲突。因此，由于必须是 的整数倍， ${\displaystyle C}$${\displaystyle \psi }$${\displaystyle \sin(kL)=0}$${\displaystyle kL}$${\displaystyle \pi }$

${\displaystyle k={\frac {n\pi }{L}}\qquad \qquad n=1,2,3,\ldots .}$

这种限制意味着对能级的限制，从而得出 ${\displaystyle k}$

${\displaystyle E_{n}={\frac {\hbar ^{2}\pi ^{2}n^{2}}{2mL^{2}}}={\frac {n^{2}h^{2}}{8mL^{2}}}.}$

有限势阱是无限势阱问题推广到具有有限深度的势阱。有限势阱问题在数学上比无限粒子盒问题更复杂，因为波函数在阱壁处不固定为零。相反，波函数必须满足更复杂的数学边界条件，因为它在阱外区域不为零。另一个相关问题是矩形势垒问题，它为量子隧穿效应提供了一个模型，而量子隧穿效应在闪存和扫描隧道显微镜等现代技术的性能中起着重要作用。

与经典情况一样，量子谐振子的势能由^{[7]给出：234}

${\displaystyle V(x)={\frac {1}{2}}m\omega ^{2}x^{2}.}$

这个问题可以通过直接求解薛定谔方程来解决，但这并不简单，也可以使用保罗·狄拉克首次提出的更优雅的“阶梯法”。本征态由下式给出

${\displaystyle \psi _{n}(x)={\sqrt {\frac {1}{2^{n}\,n!}}}\cdot \left({\frac {m\omega }{\pi \hbar }}\right)^{1/4}\cdot e^{-{\frac {m\omega x^{2}}{2\hbar }}}\cdot H_{n}\left({\sqrt {\frac {m\omega }{\hbar }}}x\right),\qquad }$

${\displaystyle n=0,1,2,\ldots .}$

其中H _n是Hermite 多项式

${\displaystyle H_{n}(x)=(-1)^{n}e^{x^{2}}{\frac {d^{n}}{dx^{n}}}\left(e^{-x^{2}}\right),}$

相应的能级为

${\displaystyle E_{n}=\hbar \omega \left(n+{1 \over 2}\right).}$

这是另一个说明束缚态能量离散化的例子。

马赫-曾德干涉仪(MZI) 用二维线性代数而非微分方程来说明叠加和干涉的概念。它可以看作是双缝实验的简化版本，但它本身就很有趣，例如在延迟选择量子擦除器、Elitzur-Vaidman 炸弹测试器以及量子纠缠研究中。^{[35] [36]}

我们可以模拟光子穿过干涉仪的过程，认为在每个点上光子只能处于两条路径的叠加中：“下”路径从左侧开始，直接穿过两个分束器，并终止于顶部；“上”路径从底部开始，直接穿过两个分束器，并终止于右侧。因此，光子的量子态是一个矢量，它是“下”路径和“上”路径的叠加，即对于复数。为了遵守假设，我们要求。 ${\displaystyle \psi \in \mathbb {C} ^{2}}$${\displaystyle \psi _{l}={\begin{pmatrix}1\\0\end{pmatrix}}}$${\displaystyle \psi _{u}={\begin{pmatrix}0\\1\end{pmatrix}}}$${\displaystyle \psi =\alpha \psi _{l}+\beta \psi _{u}}$${\displaystyle \alpha ,\beta }$${\displaystyle \langle \psi ,\psi \rangle =1}$${\displaystyle |\alpha |^{2}+|\beta |^{2}=1}$

两个分束器都建模为酉矩阵，这意味着当光子遇到分束器时，它要么以 的概率幅度留在原路径上，要么以 的概率幅度被反射到另一条路径上。上臂上的移相器建模为酉矩阵，这意味着如果光子在“上”路径上，它将获得 的相对相位，如果在下路径上，它将保持不变。 ${\displaystyle B={\frac {1}{\sqrt {2}}}{\begin{pmatrix}1&i\\i&1\end{pmatrix}}}$${\displaystyle 1/{\sqrt {2}}}$${\displaystyle i/{\sqrt {2}}}$${\displaystyle P={\begin{pmatrix}1&0\\0&e^{i\Delta \Phi }\end{pmatrix}}}$${\displaystyle \Delta \Phi }$

从左边进入干涉仪的光子将受到分束器、移相器和另一个分束器的作用​​，最终处于 ${\displaystyle B}$${\displaystyle P}$${\displaystyle B}$

${\displaystyle BPB\psi _{l}=ie^{i\Delta \Phi /2}{\begin{pmatrix}-\sin(\Delta \Phi /2)\\\cos(\Delta \Phi /2)\end{pmatrix}},}$

在右侧或顶部检测到的概率分别为

${\displaystyle p(u)=|\langle \psi _{u},BPB\psi _{l}\rangle |^{2}=\cos ^{2}{\frac {\Delta \Phi }{2}},}$

${\displaystyle p(l)=|\langle \psi _{l},BPB\psi _{l}\rangle |^{2}=\sin ^{2}{\frac {\Delta \Phi }{2}}.}$

因此，我们可以利用马赫-曾德尔干涉仪，通过估计这些概率来估算相移。

有趣的是，如果光子确实位于分束器之间的“下”或“上”路径中，会发生什么情况。这可以通过阻挡其中一条路径来实现，或者等效地通过移除第一个分束器（并根据需要从左侧或底部馈送光子）来实现。在这两种情况下，路径之间都不会再发生干扰，概率由给出，与相位无关。由此我们可以得出结论，光子在第一个分束器之后不会走一条或另一条路径，而是处于两条路径的真正量子叠加中。^[37]${\displaystyle p(u)=p(l)=1/2}$${\displaystyle \Delta \Phi }$

量子力学在解释宇宙的许多特征方面取得了巨大成功，包括经典方法无法解释的小尺度离散量和相互作用。^{[注 2]}量子力学通常是唯一能够揭示构成所有物质形式（电子、质子、中子、光子等）的亚原子粒子个体行为的理论。固体物理学和材料科学依赖于量子力学。^[38]

在许多方面，现代技术都在量子效应显著的规模下运行。量子理论的重要应用包括量子化学、量子光学、量子计算、超导磁体、发光二极管、光放大器和激光器、晶体管和半导体（如微处理器）、医学和研究成像（如磁共振成像和电子显微镜）。^[39]许多生物和物理现象的解释都源于化学键的性质，最著名的是大分子DNA。

Modern physics
${\displaystyle {\hat {H}}|\psi _{n}(t)\rangle =i\hbar {\frac {d}{dt}}|\psi _{n}(t)\rangle }$ ${\displaystyle G_{\mu \nu }+\Lambda g_{\mu \nu }={\kappa }T_{\mu \nu }}$ Schrödinger and Einstein field equations
Founders Max Planck Albert Einstein Niels Bohr Max Born Erwin Schrödinger Werner Heisenberg Pascual Jordan Wolfgang Pauli Paul Dirac Ernest Rutherford Louis de Broglie Satyendra Nath Bose
Concepts Topology Space Time Energy Matter Work Randomness Information Entropy Light Particle Wave
Branches Applied Experimental Theoretical Mathematical Philosophy of physics Quantum mechanics Quantum field theory Quantum information Quantum computation Electromagnetism Weak interaction Electroweak interaction Strong interaction Atomic Particle Nuclear Atomic, molecular, and optical Condensed matter Statistical Complex systems Non-linear dynamics Biophysics Neurophysics Plasma physics Special relativity General relativity Astrophysics Cosmology Theories of gravitation Quantum gravity Theory of everything
Scientists Röntgen Witten Becquerel Lorentz Planck Curie Wien Skłodowska-Curie Sommerfeld Rutherford Soddy Onnes Einstein Wilczek Born Weyl Bohr Kramers Schrödinger de Broglie Laue Bose Compton Pauli Walton Fermi van der Waals Heisenberg Dyson Zeeman Moseley Hilbert Gödel Jordan Dirac Wigner Hawking P. W. Anderson Lemaître Thomson Poincaré Wheeler Penrose Millikan Nambu von Neumann Higgs Hahn Feynman Yang Lee Lenard Salam 't Hooft Veltman Bell Gell-Mann J. J. Thomson Raman Bragg Bardeen Shockley Chadwick Lawrence Zeilinger Goudsmit Uhlenbeck
Categories Modern physics
v t e

量子力学规则断言，系统的状态空间是希尔伯特空间，系统的可观测量是作用于该空间中向量的厄米算子——尽管它们没有告诉我们是哪个希尔伯特空间或哪个算子。可以通过适当选择这些来获得量子系统的定量描述，这是做出物理预测的必要步骤。做出这些选择的重要指南是对应原理，这是一种启发式方法，它指出，在量子数较大的区域，量子力学的预测可以简化为经典力学的预测。^[40]人们也可以从某个特定系统的已建立的经典模型开始，然后试着猜测在对应极限下会产生经典模型的底层量子模型。这种方法称为量化。^{[41] : 299  [42]}

量子力学最初被提出时，它被应用于对应极限为非相对论经典力学的模型。例如，众所周知的量子谐振子模型对振荡器的动能使用了明确的非相对论表达式，因此是经典谐振子的量子版本。^{[7] : 234}

混沌系统没有好的量子数，因此会出现复杂情况，量子混沌研究这些系统中经典描述和量子描述之间的关系。^{[41] : 353}

量子退相干是一种量子系统失去相干性的机制，因此无法显示许多典型的量子效应：量子叠加变成简单的概率混合，量子纠缠变成简单的经典关联。^{[7] ：687–730}量子相干性在宏观尺度上通常并不明显，但在接近绝对零度的温度下，量子行为可能在宏观上表现出来。^{[注 3]}

经典系统的许多宏观性质都是其各部分的量子行为的直接结果。例如，块状物质（由原子和分子组成，仅在电力作用下就会迅速坍缩）的稳定性、固体的刚性以及物质的机械、热、化学、光学和磁性都是电荷在量子力学规则下相互作用的结果。 [ ^43]

早期将量子力学与狭义相对论相结合的尝试包括用协变方程（如克莱因-戈登方程或狄拉克方程）替换薛定谔方程。虽然这些理论成功地解释了许多实验结果，但它们忽略了粒子的相对论性产生和湮灭，因此存在某些不尽人意之处。完全相对论性的量子论需要发展量子场论，它将量化应用于场（而不是一组固定的粒子）。第一个完整的量子场论是量子电动力学，它对电磁相互作用提供了完全量子的描述。量子电动力学和广义相对论一样，是迄今为止最精确的物理理论之一。^{[44] [45]}

描述电动力学系统通常不需要完整的量子场论装置。一种更简单的方法是将带电粒子视为受经典电磁场作用的量子力学物体，这种方法自量子力学诞生以来就一直被使用。例如，氢原子的基本量子模型使用经典的库仑势来描述氢原子的电场。^{[7] : 285}同样，在斯特恩-格拉赫实验中，带电粒子被建模为量子系统，而背景磁场则用经典方式描述。^{[41] : 26}如果电磁场中的量子涨落起着重要作用，例如带电粒子发射光子，这种“半经典”方法就会失败。 ${\displaystyle \textstyle -e^{2}/(4\pi \epsilon _{_{0}}r)}$

强核力和弱核力的量子场论也已发展起来。强核力的量子场论称为量子色动力学，描述夸克和胶子等亚核粒子的相互作用。物理学家阿卜杜斯·萨拉姆、谢尔登·格拉肖和史蒂芬·温伯格将弱核力和电磁力以量化形式统一为单一量子场论（称为电弱理论）。^[46]

尽管量子理论和广义相对论的预测都得到了严格和反复的经验证据的支持，但它们的抽象形式却相互矛盾，而且事实证明，它们极难整合成一个一致、有凝聚力的模型。在粒子物理学的许多领域，引力可以忽略不计，因此在这些特定应用中，广义相对论和量子力学之间的统一并不是一个紧迫的问题。然而，缺乏正确的量子引力理论是物理宇宙学和物理学家寻找优雅的“万物理论”（TOE）的一个重要问题。因此，解决这两种理论之间的不一致一直是 20 世纪和 21 世纪物理学的主要目标。这种 TOE 不仅会结合亚原子物理模型，还会从单一的力或现象中推导出自然界的四种基本力。^[47]

一种实现这一目标的提议是弦理论，它假定粒子物理学中的点状粒子被称为弦的一维物体。弦理论描述了这些弦如何在空间中传播并相互作用。在大于弦尺度的距离尺度上，弦看起来就像一个普通粒子，其质量、电荷和其他属性由弦的振动状态决定。在弦理论中，弦的许多振动状态之一对应于引力子，一种携带引力的量子力学粒子。^{[48] [49]}

另一个流行的理论是圈量子引力(LQG)，它描述了引力的量子特性，因此是一种量子时空理论。圈量子引力试图融合和调整标准量子力学和标准广义相对论。该理论将空间描述为由有限圈“编织”而成的极细织物，称为自旋网络。自旋网络随时间的演变称为自旋泡沫。自旋泡沫的特征长度尺度是普朗克长度，约为 1.616×10 ⁻³⁵米，因此短于普朗克长度的长度在圈量子引力中没有物理意义。^[50]

自诞生以来，量子力学的许多反直觉方面和结果引发了激烈的哲学争论和许多解释。争论集中在量子力学的概率性质、波函数坍缩的困难和相关的测量问题以及量子非局域性上。关于这些问题，也许唯一的共识就是没有共识。理查德·费曼曾经说过：“我想我可以肯定地说，没有人理解量子力学。” ^[51]根据史蒂芬·温伯格的说法，“在我看来，现在还没有完全令人满意的量子力学解释。” ^[52]

尼尔斯·玻尔、维尔纳·海森堡和其他物理学家的观点通常被归为“哥本哈根诠释”。^{[53] [54]}根据这些观点，量子力学的概率性质并不是最终会被确定性理论取代的暂时特征，而是对经典“因果关系”观念的最终放弃。玻尔特别强调，任何明确定义的量子力学形式主义的应用都必须始终参考实验安排，因为在不同实验情况下获得的证据具有互补性。诺贝尔量子物理学奖获得者采用了哥本哈根式的诠释，包括玻尔、^[55]海森堡、^[56]薛定谔、^[57]费曼、^[2]和蔡林格^[58]以及 21 世纪量子基础研究人员。^[59]

阿尔伯特·爱因斯坦是量子理论的创始人之一，他对于量子理论明显未能尊重一些珍贵的形而上学原理，如决定论和局域性，感到困扰。爱因斯坦与玻尔关于量子力学的意义和地位的长期交流，现在被称为玻尔-爱因斯坦辩论。爱因斯坦认为，量子力学的基础必须是一种明确禁止超距作用的理论。他认为量子力学是不完整的，是一种有效但不是基本理论，类似于热力学的有效性，但其背后的基本理论是统计力学。1935 年，爱因斯坦与他的合作者鲍里斯·波多尔斯基和内森·罗森发表了一个论点，认为局域性原理意味着量子力学的不完备性，这个思想实验后来被称为爱因斯坦-波多尔斯基-罗森悖论。^{[注 4]} 1964 年，约翰·贝尔 (John Bell)证明 EPR 的局域性原理和决定论实际上与量子力学不相容：它们对距离系统产生的相关性施加了约束，现在称为贝尔不等式，而纠缠粒子可能会违反这些约束。^[64]此后，人们进行了多项实验来获得这些相关性，结果表明它们确实违反了贝尔不等式，从而证伪了局域性和决定论的结合。^{[16] [17]}

玻姆力学表明，可以重新表述量子力学，使其具有确定性，但代价是使其具有明确的非局部性。它不仅将波函数归因于物理系统，还将一个实位置归因于物理系统，该位置在非局部引导方程下确定性地演化。物理系统的演化始终由薛定谔方程和引导方程给出；波函数永远不会崩溃。这解决了测量问题。^[65]

埃弗里特于 1956 年提出的多重世界诠释认为，量子理论描述的所有可能性都会同时发生在由大多数独立的平行宇宙组成的多元宇宙中。^[66]这是去除波包坍缩公理的结果。被测系统、测量仪器和观察者的所有可能状态都存在于真实的物理量子叠加中。虽然多元宇宙是确定性的，但我们感知到的是由概率支配的非确定性行为，因为我们不是观察整个多元宇宙，而是一次只观察一个平行宇宙。这究竟如何运作一直是争论的焦点。人们曾多次尝试理解这一理论并推导出玻恩规则，^{[67] [68]}但对于他们是否成功并没有达成共识。^{[69] [70] [71]}

关系量子力学作为哥本哈根式思想的现代衍生物于 20 世纪 90 年代末出现，^[72]几年后，QBism也得到了发展。 ^[73]

量子力学是在 20 世纪初期发展起来的，其驱动力是解释一些早期观测到的现象。对光的波动性的科学研究始于 17 和 18 世纪，当时罗伯特·胡克、克里斯蒂安·惠更斯和莱昂哈德·欧拉等科学家根据实验观察提出了光的波动理论。^[74] 1803 年，英国博学家 托马斯·杨描述了著名的双缝实验。^{[75]这个实验}对光的波动理论的普遍接受起到了重要作用。

19 世纪初，约翰·道尔顿和阿梅代奥·阿伏伽德罗的化学研究为物质的原子理论增添了分量，詹姆斯·克拉克·麦克斯韦、路德维希·玻尔兹曼等人在此基础上建立了气体动能论。动能论的成功进一步证实了物质由原子组成的观点，但该理论也有缺点，只有通过量子力学的发展才能解决。^{[76]虽然早期}希腊哲学对原子的概念是它们是不可分割的单位（“原子”一词源于希腊语，意为“不可切割的”——但 19 世纪人们形成了关于亚原子结构的假设。这方面的一个重要发现是迈克尔·法拉第1838 年观察到低压气体玻璃管内放电引起的辉光。尤利乌斯·普吕克、约翰·威廉·希托夫和尤金·戈德斯坦继续并改进了法拉第的工作，发现了阴极射线，JJ·汤姆森发现阴极射线是由被称为电子的亚原子粒子组成。^{[77] [78]}

黑体辐射问题由古斯塔夫·基尔霍夫于 1859 年发现。1900 年，马克斯·普朗克提出假设，认为能量以离散的“量子”（或能量包）的形式辐射和吸收，计算结果与观察到的黑体辐射模式精确匹配。^[79]量子一词源于拉丁语，意为“有多大”或“多少”。^[80]根据普朗克的说法，能量可以分为“元素”，其大小（E ）与其频率（ν ）成正比：

${\displaystyle E=h\nu \ }$，

其中h是普朗克常数。普朗克谨慎地坚持认为这只是辐射吸收和发射过程的一个方面，而不是辐射的物理现实。 ^[81]事实上，他认为他的量子假设是为了得到正确答案而使用的数学技巧，而不是一项重大发现。^[82]然而，1905 年，阿尔伯特·爱因斯坦现实地解释了普朗克的量子假设，并用它来解释光电效应，即光照射到某些材料上会从材料中弹出电子。尼尔斯·玻尔随后将普朗克关于辐射的思想发展成氢原子模型，并成功预测了氢的光谱线。 ^[83]爱因斯坦进一步发展了这个想法，表明电磁波（如光）也可以描述为粒子（后来称为光子），其离散能量取决于其频率。^[84]在他的论文《论辐射的量子理论》中，爱因斯坦扩展了能量与物质之间的相互作用，以解释原子对能量的吸收和发射。尽管当时被他的广义相对论所掩盖，这篇论文阐明了受激发射辐射的机制^[85] ，这成为了激光的基础。^[86]

这一阶段被称为旧量子理论。旧量子理论从来都不是完整的，也不自洽的，而是一系列对经典力学的启发式修正。^{[87] [88]}现在，该理论被理解为现代量子力学的半经典近似。^{[89] [90]}除了上面提到的普朗克、爱因斯坦和玻尔的工作外，这一时期的显著成果还包括爱因斯坦和彼得·德拜关于固体比热容的工作，玻尔和亨德利卡·约翰娜·范莱文证明经典物理无法解释抗磁性，以及阿诺德·索末菲对玻尔模型的扩展，使其包括狭义相对论效应。^{[87] [91]}

20 世纪 20 年代中期，量子力学发展成为原子物理学的标准表述。1923 年，法国物理学家路易·德布罗意提出了物质波理论，指出粒子可以表现出波的特性，反之亦然。在德布罗意的方法的基础上，现代量子力学于 1925 年诞生。当时，德国物理学家维尔纳·海森堡、马克斯·玻恩和帕斯夸尔·约当^{[92] [93]}发展了矩阵力学，奥地利物理学家埃尔温·薛定谔发明了波力学。1926 年 7 月，玻恩引入了薛定谔波函数的概率解释。^[94]因此，整个量子物理学领域应运而生，并在 1927 年的第五届索尔维会议上得到了更广泛的认可。 ^[95]

到 1930 年，量子力学由大卫·希尔伯特、保罗·狄拉克和约翰·冯·诺依曼进一步统一和形式化^[96]，更加强调测量、我们对现实知识的统计性质以及对“观察者”的哲学推测。此后，量子力学渗透到许多学科，包括量子化学、量子电子学、量子光学和量子信息科学。它还为现代元素周期表的许多特征提供了有用的框架，描述了原子在化学键合过程中的行为以及计算机半导体中电子的流动，因此在许多现代技术中发挥着至关重要的作用。虽然量子力学是为描述微小世界而构建的，但它也需要解释一些宏观现象，如超导体^[97]和超流体。^[98]

• J. O'Connor 和 EF Robertson：量子力学的历史。
• Quantiki 的量子理论简介。
• 量子物理学变得相对简单：汉斯·贝特 (Hans Bethe)的三个视频讲座。

课程材料

• 量子食谱和 PHYS 201：物理学基础 II，作者：Ramamurti Shankar，耶鲁大学开放式课程。
• 现代物理学：包括波、热力学和光学——一本在线教科书。
• MIT 开放式课程：化学和物理。参见 8.04、8.05 和 8.06。
• .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠5+1/2⁠ 量子力学中的例子。
• 帝国理工学院量子力学课程。

哲学

• Ismael, Jenann。《量子力学》。收录于Zalta, Edward N. (编)。斯坦福哲学百科全书。
• Krips, Henry。《量子理论中的测量》。收录于Edward N. Zalta主编。《斯坦福哲学百科全书》 。