百分位数

在统计学中，k百分 位数，也称为百分位数分数或百分位数，是频率分布中给定百分比k的分数低于该分数 （“排他性”定义），或给定百分比的分数等于或低于该分数（“包含性”定义）；也就是说， k百分位数中的分数将高于其集合中所有分数的约k %。百分位数以与输入分数相同的计量单位表示，而不是百分比；例如，如果分数指的是人的体重，则相应的百分位数将以公斤或磅表示。在无限样本量的限制下，百分位数近似于百分位数函数，即累积分布函数的倒数。

百分位数是一种分位数，通过细分为 100 个组获得。第 25 个百分位数也称为第一四分位数( Q ₁ )，第 50 个百分位数称为中位数或第二四分位数 ( Q ₂ )，第 75 个百分位数称为第三四分位数 ( Q ₃ )。例如，第 50 个百分位数（中位数）是分布中 50% 的分数 低于（或等于或低于，取决于定义）的分数。

一个相关量是分数的百分位等级，以百分比表示，表示分数分布中低于它的分数的比例，这是一种排他性定义。百分位分数和百分位等级通常用于报告常模参照测验的测试分数，但是，正如刚才提到的，它们并不相同。对于百分位等级，会给出一个分数并计算一个百分比。百分位等级是排他性的：如果某个指定分数的百分位等级是 90%，那么 90% 的分数低于该分数。相反，对于百分位数，会给出一个百分比并确定相应的分数，该分数可以是排他性的，也可以是包含性的。指定百分比（例如 90 分）的分数表示分布中其他分数低于某个分数（排他性定义）或等于或低于该分数（包含性定义）。

百分位数没有标准的定义；^{[1] [2] [3]} 但是，当观测值数量非常大且概率分布是连续的时，所有定义都会产生类似的结果。^[4]在极限情况下，当样本量趋近于无穷大时，第 100 个^p百分位数 (0< p <1) 近似于这样形成的累积分布函数(CDF) 的倒数，在p处求值，因为p近似于 CDF。这可以看作是Glivenko-Cantelli 定理的结果。下面给出了一些计算百分位数的方法。

计算方法部分 (下文)中给出的方法是用于小样本统计的近似值。一般而言，对于服从正态分布的非常大的总体，百分位数通常可以参考正态曲线图来表示。正态分布沿缩放到标准差或 sigma ( ) 单位的轴绘制。从数学上讲，正态分布左侧延伸到负无穷，右侧延伸到正无穷。但请注意，总体中只有极小部分个体会超出 −3 σ到 +3 σ的范围。例如，对于人类身高，很少有人的身高水平高于 +3 σ。 ${\displaystyle \sigma}$

百分位数表示正态曲线下的面积，从左到右逐渐增大。每个标准差代表一个固定的百分位数。因此，四舍五入到小数点后两位，−3 σ表示第 0.13 百分位数，−2 σ表示第 2.28 百分位数，−1 σ表示第 15.87 百分位数，0 σ表示第 50 百分位数（分布的平均值和中位数），+1 σ表示第 84.13 百分位数，+2 σ表示第 97.72 百分位数，+3 σ表示第 99.87 百分位数。这与68–95–99.7 规则或三西格玛规则有关。请注意，理论上，0 百分位数位于负无穷大，100 百分位数位于正无穷大，但在许多实际应用中（例如测试结果），会强制执行自然的下限和/或上限。

当ISP对“突发”互联网带宽进行计费时，第 95 或第 98 个百分位通常会截断每月带宽峰值的前 5% 或 2%，然后以最接近的费率计费。这样，不频繁的峰值将被忽略，并以更公平的方式向客户收费。此统计数据在测量数据吞吐量方面非常有用，因为它可以非常准确地反映带宽成本。第 95 个百分位表示，95% 的时间，使用量低于此数量：因此，其余 5% 的时间，使用量高于该数量。

医生通常会使用婴儿和儿童的体重和身高来评估他们的生长情况，并与生长图表中的全国平均值和百分位数进行比较。

道路上第 85 百分位车速通常被用作制定速度限制的指导方针，并评估该限制是否过高或过低。^{[5] [6]}

在金融领域，风险价值是一种标准衡量标准，用于评估（以模型相关的方式）在给定的置信值下，投资组合的价值在给定时间段内预计不会下降的数量。

10 分分布的插值和最接近秩、独占和包含百分位数

百分位数得分有许多公式或算法^{[7] 。Hyndman 和 Fan [1]}确定了九种，大多数统计和电子表格软件都使用他们描述的方法之一。^[8]算法要么返回得分集中存在的得分值（最近排序法），要么在现有得分之间进行插值，并且要么是独占的，要么是包含的。

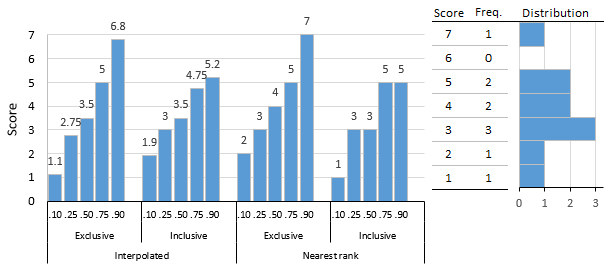
该图显示了 10 分分布，说明了这些不同算法产生的百分位数分数，并作为后续示例的介绍。最简单的方法是返回分布分数的最近排序方法，尽管与插值方法相比，结果可能有点粗糙。最近排序方法表显示了排他和包容方法的计算步骤。

插值方法，顾名思义，可以返回分布分数之间的分数。统计程序使用的算法通常使用插值方法，例如 Microsoft Excel 中的 percentile.exc 和 percentile.inc 函数。插值方法表显示了计算步骤。

百分位数的一个定义（通常在文本中给出）是，N 个有序值（从最小到最大排序）列表的第P个百分位数是列表中的最小值，其中不超过P % 的数据严格小于该值，至少有P % 的数据小于或等于该值。这是通过首先计算序数等级，然后从与该等级相对应的有序列表中获取值来获得的。序数等级n​​使用以下公式计算 ${\displaystyle (0<P\leq 100)}$

${\displaystyle n=\left\lceil {\frac {P}{100}}\times N\right\rceil .}$

• 对包含少于 100 个不同值的列表使用最近排序法可能会导致相同的值被用于超过一个百分位数。
• 使用最近排序法计算的百分位数将始终是原始有序列表的成员。
• 第 100 个百分位数被定义为有序列表中的最大值。

在许多应用程序中使用的舍入的替代方法是在相邻等级之间使用线性插值。

以下所有变体都有以下共同点。给定顺序统计量

${\displaystyle \{v_{i},i=1,2,\ldots ,N:v_{i+1}\geq v_{i},\forall i=1,2,\ldots ,N-1\},}$

我们寻找一个通过这些点的线性插值函数。这可以通过以下方式轻松实现 ${\displaystyle (v_{i},i)}$

${\displaystyle v(x)=v_{\lfloor x\rfloor }+(x{\bmod {1}})(v_{\lfloor x\rfloor +1}-v_{\lfloor x\rfloor }),\forall x\in [1,N]:v(i)=v_{i}{\text{, for }}i=1,2,\ldots ,N,}$

其中，使用floor 函数表示正x的整数部分，而使用mod 函数表示其小数部分（除以 1 后的余数）。 （请注意，尽管在端点 处未定义，但没有必要定义，因为它乘以了。）我们可以看出，x是下标i的连续版本，在相邻节点之间线性插入v。 ${\displaystyle \lfloor x\rfloor }$${\displaystyle x{\bmod {1}}}$${\displaystyle x=N}$${\displaystyle v_{\lfloor x\rfloor +1}}$${\displaystyle x{\bmod {1}}=0}$

变体方法有两点不同。第一种是秩x 、百分比秩和与样本大小 N有关的常数之间的线性关系： ${\displaystyle P=100p}$

${\displaystyle x=f(p,N)=(N+c_{1})p+c_{2}.}$

还有一个附加要求，即对应于中位数的范围中点出现在： ${\displaystyle (1,N)}$${\displaystyle p=0.5}$

${\displaystyle {\begin{aligned}f(0.5,N)&={\frac {N+c_{1}}{2}}+c_{2}={\frac {N+1}{2}}\\\therefore 2c_{2}+c_{1}&=1\end{aligned}},}$

修改后的函数现在只有一个自由度，如下所示：

${\displaystyle x=f(p,N)=(N+1-2C)p+C.}$

变体之间的第二个不同之处在于函数在p的范围边缘附近的定义：应该产生或被迫产生在范围内的结果，这可能意味着在更宽的区域中不存在一一对应的关系。一位作者建议选择其中ξ是广义极值分布的形状，它是抽样分布的极值极限。 ${\displaystyle [0,1]}$${\displaystyle f(p,N)}$${\displaystyle [1,N]}$${\displaystyle C={\tfrac {1}{2}}(1+\xi )}$

（来源：Matlab“prctile”函数，^{[9] [10]}）

${\displaystyle x=f(p)={\begin{cases}Np+{\frac {1}{2}},\forall p\in \left[p_{1},p_{N}\right],\\1,\forall p\in \left[0,p_{1}\right],\\N,\forall p\in \left[p_{N},1\right].\end{cases}}}$

在哪里

${\displaystyle p_{i}={\frac {1}{N}}\left(i-{\frac {1}{2}}\right),i\in [1,N]\cap \mathbb {N} }$

${\displaystyle \therefore p_{1}={\frac {1}{2N}},p_{N}={\frac {2N-1}{2N}}.}$

此外，让

${\displaystyle P_{i}=100p_{i}.}$

反比关系被限制在一个较窄的区域内：

${\displaystyle p={\frac {1}{N}}\left(x-{\frac {1}{2}}\right),x\in (1,N)\cap \mathbb {R} .}$

[来源：一些软件包，包括NumPy ^[11]和Microsoft Excel ^[3]（截至 2013 版，使用 PERCENTILE.INC 函数）。NIST 将其列为替代方案。 [ ^8] ]

${\displaystyle x=f(p,N)=p(N-1)+1{\text{, }}p\in [0,1]}$

${\displaystyle \therefore p={\frac {x-1}{N-1}}{\text{, }}x\in [1,N].}$

请注意，对于 来说，关系是一对一的，它是三个变体中唯一一个具有此属性的变体；因此，在 Excel 函数中， 包含 的后缀为“INC”。${\displaystyle x\leftrightarrow p}$${\displaystyle p\in [0,1]}$

（ NIST推荐的主要变体。^[8]自 2010 年起，Microsoft Excel 通过 PERCENTIL.EXC 函数采用该变体。但是，正如“EXC”后缀所示，Excel 版本排除了p范围的两个端点，即，而第二个变体“INC”版本则没有这样做；事实上，任何小于 的数字也会被排除，并且会导致错误。） ${\displaystyle p\in (0,1)}$${\displaystyle {\frac {1}{N+1}}}$

${\displaystyle x=f(p,N)={\begin{cases}1{\text{, }}p\in \left[0,{\frac {1}{N+1}}\right]\\p(N+1){\text{, }}p\in \left({\frac {1}{N+1}},{\frac {N}{N+1}}\right)\\N{\text{, }}p\in \left[{\frac {N}{N+1}},1\right]\end{cases}}.}$

逆运算被限制在一个较窄的区域：

${\displaystyle p={\frac {x}{N+1}}{\text{, }}x\in (0,N).}$

除了百分位数函数外，还有加权百分位数，其中计算的是总权重中的百分比，而不是总数。加权百分位数没有标准函数。一种方法以自然的方式扩展了上述方法。

假设我们有与N 个排序样本值分别相关的正权重。让 ${\displaystyle w_{1},w_{2},w_{3},\dots ,w_{N}}$

${\displaystyle S_{N}=\sum _{k=1}^{N}w_{k},}$

权重之和。然后上述公式可以推广为

${\displaystyle p_{n}={\frac {1}{S_{N}}}\left(S_{n}-{\frac {w_{n}}{2}}\right)}$什么时候，${\displaystyle C=1/2}$

或者

${\displaystyle p_{n}={\frac {S_{n}-Cw_{n}}{S_{N}+(1-2C)w_{n}}}}$对于一般来说，${\displaystyle C}$

和

${\displaystyle v=v_{k}+{\frac {P-p_{k}}{p_{k+1}-p_{k}}}(v_{k+1}-v_{k}).}$

50% 的加权百分位数称为加权中位数。

• 十分位
• 百分位排名
• 分位数
• 汇总统计